X.24.8.2 Distribuţia Maxwell

Pentru mediul atomic (pentru simplitate considerăm cazul unui gaz inert, ce nu formează molecule), atributul de stare al energiei ce revine unui element (considerând masele egale pentru toţi atomii) este viteza, şi fiind vorba de energie, este important numai modulul acestei viteze. Fiind vorba de modulul vitezei atomilor, în cazul unui mediu aflat la o anumită temperatură ştim că există o distribuţie a acestui modul pe mulţimea totală a atomilor, distribuţia Maxwell.

Comentariul X.24.8.2.1: Dacă ţinem cont de definiţia obiectului abstract distribuţie dată în cap. 2 al acestei lucrări şi identificăm conform acestei definiţii care este atributul suport şi care cel distribuit, în cazul distribuţiei Maxwell vom constata că viteza este atributul suport (variabila independentă) iar atributul distribuit (dependent) este numărul de atomi (populaţia atomică) ce au viteza cuprinsă în intervalul suport elementar. Aşadar nu putem vorbi de distribuţia vitezei atomilor (pentru că nu viteza este atributul distribuit) ci de distribuţia numărului de atomi pe domeniul suport modulul vitezei acestora. Dacă ţinem cont că de fapt distribuţia în funcţie de viteză este o reprezentare a distribuţiei impulsurilor atomilor, putem spune că de fapt distribuţia Maxwell este o precursoare a distribuţiei energetice a atomilor unui mediu, în acest caz energia cinetică fiind atributul suport al distribuţiei. De asemenea, atributul suport (viteza) în cazul distribuţiei Maxwell are ca domeniu de valori segmentul pozitiv al axei numerelor reale, aşadar o mulţime continuă, în timp ce atributul distribuit (mulţimea finită a atomilor mediului) are ca valori un segment pozitiv al mulţimii numerelor întregi (numere naturale) aşadar o mulţime discretă. Totuşi, deoarece numerele de atomi implicate în distribuţie sunt foarte mari şi ele nu por fi scrise decât folosind notaţia ştiinţifică (cu mantisă zecimală şi exponent) şi domeniul valorii distribuite pare continuu.

Densitatea acestei distribuţii pe un domeniu suport elementar de mărime dv şi cu referinţa internă la valoarea  (densitate care înseamnă numărul de atomi ce au viteza inclusă în domeniul suport corespondent) este (conform manualelor de fizică statistică[1]):

                                                                                       (X.24.8.2.1)

unde

                                                                                                             (X.24.8.2.2)

iar

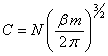                                                                                                  (X.24.8.2.3)

 

N fiind numărul total de atomi din mediu, m masa atomilor, T  temperatura mediului şi k fiind constanta lui Boltzmann. Dacă în relaţia X.24.8.2.1 facem (similar ca în cazul distribuţiei Plank) schimbarea de variabilă:

                                                                                                   (X.24.8.2.4)

 

unde x este tot o mărime scalară (raportul a două energii per element, cea cinetică şi cea termică), vom obţine distribuţia Maxwell normalizată:

                                                                              (X.24.8.2.5)

 

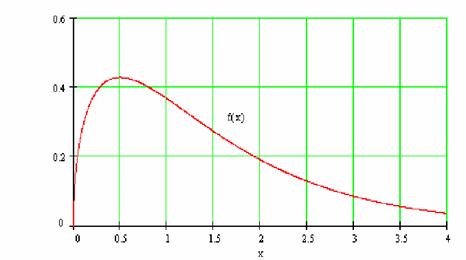
Fig. X.24.8.2.1

unde  este reprezentată în fig. X.24.8.2.1, cu un maxim la valoarea x_R=0.5 (referinţa internă a distribuţiei normalizate), adică în situaţia când energia cinetică de translaţie liberă pe element de mediu atomic G (ce corespunde densităţii distribuţiei acestei energii pe mulţimea atomilor) este jumătate din energia kT, conţinută în mediul fotonic la echilibru. Acest fapt ne arată că pentru a exista un echilibru între densitatea de energie termică (ce are atât componenta T[2] cât şi cea R), şi densitatea energiei cinetice a atomilor, restul energiei termice (componenta R a fotonilor) trebuie să fie în echilibru cu componenta R a energiei cinetice (tot libere) a atomilor.

 

Comentariul X.24.8.2.2: După clasificarea mediilor în cele trei clase fundamentale S, L şi G, ştim acum că energie de translaţie liberă pot avea numai elementele mediilor G, astfel că energia termică din mediul fotonic intern se va repartiza în cazul acestor medii celor două tipuri posibile de energie cinetică (T şi R). în cazul mediilor L nu mai este permisă translaţia liberă, aşa că energia termică va trebui să fie în echilibru doar cu energia cinetică (cvasiliberă) R a atomilor şi cu energia de vibraţie forţată T. în cazul mediilor S, unde nu este permisă nici mişcarea liberă R, energia termică va fi în echilibru doar cu energiile vibraţionale forţate (atât T cât şi R). Afirmaţiile de mai sus sunt valabile în cazul mediilor atomice; în cazul mediilor moleculare, la vibraţiile intermoleculare se mai adaugă cele intramoleculare, fiecare cu energiile lor atât T cât şi R.

 

Aşa cum am văzut în paragrafele anterioare, densitatea energiei termice (densitatea FE stocastic fotonic) într-un anumit mediu, nu depinde de tipul mediului, ci numai de temperatura acestuia, energia termică fiind conţinută exclusiv în mediul interstiţial al fotonilor termici. Condiţia ca această densitate de flux să fie în echilibru cu densitatea fluxurilor cinetice per element ale mediului atomic sau molecular, face însă ca acest echilibru să fie atins în condiţii diferite, la aceeaşi cantitate de energie termică introdusă, parametrii cinetici ai elementelor mediului şi temperatura de echilibru fiind funcţie de tipul mediului. Cu alte cuvinte, într-un mediu (să zicem atomic) aflat teoretic la temperatura de zero absolut (adică în interiorul său nu există fotoni termici), dacă injectăm o cantitate de energie termică (un flux extern de fotoni termici), în cazul că pierderile de căldură ale mediului sunt neglijabile, această energie termică se va distribui prin interacţiuni repetate între mediul fotonic şi mediul atomic. în urma acestei autodistribuiri, la atingerea stării de echilibru dintre fluxul stocastic fotonic şi cel stocastic atomic, vom avea (în funcţie de tipul de mediu S, L sau G) mai multe categorii de energie:

-     Energie termică (evidenţiată prin temperatură) ;

-     Energie T liberă (evidenţiată prin presiune şi existentă numai în mediile G) ;

-     Energie R liberă (existentă doar la mediile G şi L)

-     Energie vibraţională (T şi/sau R în funcţie de tipul de mediu G, L sau S).

Evident, suma tuturor acestor componente energetice va fi egală cu cantitatea de energie termică introdusă iniţial şi presupusă conservată în mediu

.

Comentariul X.24.8.2.3: Discuţia de mai sus asupra distribuirii energiei termice în alte forme de energie este independentă de tipul de atomi ce formează mediul atomic, dar trebuie făcută o remarcă importantă. în funcţie de cantitatea de căldură introdusă în mediul atomic, în urma distribuirii acesteia în toate formele de energie posibile menţionate mai sus, tipul de atom ce formează mediul este determinant în ce priveşte clasa de mediu (S, L, G) ce va rezulta în momentul atingerii echilibrului termic. Această dependenţă se datorează distribuţiei spaţiale neuniforme (cu excepţia atomilor gazelor inerte) a orbitalilor electronici de pe ultima pătură (cea externă), distribuţie care va determina una sau mai multe direcţii preferenţiale ale viitoarelor interacţiuni cu ceilaţi atomi. Cu cât aceste interacţiuni vor fi mai direcţionale şi mai puternice, cu atât posibilităţile de rotaţie ulterioară a elementelor vor fi mai reduse (de exemplu cazul metalelor greu fuzibile sau al carbonului).

 

Trebuie să subliniem explicit că distribuţia Maxwell este valabilă numai pentru mediile G, deoarece aşa cum menţionam mai sus, doar în aceste medii poate exista translaţie liberă a elementelor mediului. în celelalte clase de medii (S, L) pot exista doar translaţii forţate (vibratorii, deoarece interacţiunile între elemente sunt permanente). Faptul că s-a determinat distribuţia vitezelor pentru atomii sau moleculele unor solide sau lichide nu înseamnă decât că acea distribuţie era valabilă în faza de vapori a substanţelor respective.

 

Comentariul X.24.8.2.4: Nici nu se putea altfel, deoarece selectorul de viteză pentru determinarea vitezelor atomice sau moleculare nu funcţionează decât cu fascicule atomice sau moleculare (fascicule de elemente singulare ale substanţei) provenite din faza gazoasă a substanţei de analiză.