X.3.2.3 Derivata în sens obiectual

Esenţa abordării obiectuale (sistemice) constă în organizarea informaţiei de prelucrat în obiecte şi procese folosind noţiunea de distribuţie. De asemenea se urmăreşte identificarea atributelor de model ale obiectelor după modelul general de obiect dat în cap. 3, iar dacă există procese, identificarea obiectelor procesuale. în cazul mulţimilor de obiecte între care există relaţii externe (cazul obiectelor compuse), ştim de asemenea că aceste relaţii există între referinţele interne ale obiectelor, referinţele interne fiind substitute ale obiectelor în aceste relaţii,  deoarece relaţii cantitative pot există doar între valori singulare.

Conform celor stabilite în cap. 2, relaţia y=f(x) menţionată la începutul par. X.3.2.2 constiuie distribuţia atributului y pe atributul suport x, în varianta în care relaţia de atribuire este invariantă (o funcţie) pe întreg domeniul suport (domeniul de continuitate al funcţiei). Tot în cap. 2 am văzut că pentru o valoare singulară considerată invariantă x_k, şi valoarea atributului distribuit y_k este invariantă, aşa că valorile y_k distribuite pe valorile x_k le recunoaştem uşor ca fiind obiecte abstracte din clasa S₀. Un cuplu  căruia îi corespunde pe graficul din fig. X.3.2.3.1 punctul P_k cu vectorul de poziţie r_k, este un element al mulţimii relaţiilor de atribuire ce formează distribuţia (adică un element al distribuţiei primare).

Dacă avem două variaţii simetrice ale atributului suport de la valoarea  până la  faţă de valoarea singulară x_k (la valorile cărora vom avea punctele, respectiv ), suficient de mici încât distribuţiile pe ele să poată fi considerate liniare, acestora le vor corespunde variaţiile de atribut:

                                                               (X.3.2.3.1)

şi:

                                                               (X.3.2.3.2)

 

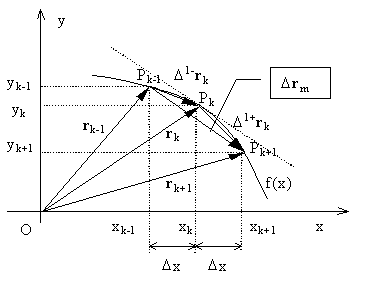
Fig. X.3.2.3.1

Conform celor convenite în cap. 2, 3 şi 4, relaţia:

                                                     (X.3.2.3.3)

 

identică cu relaţia X.3.2.2.3, înseamnă densitatea uniformă a unei distribuţii liniare a variaţiei de atribut  pe un interval suport  (adică densitatea unui PES de tip P₁) evaluată la stânga referinţei x_k. Am văzut în cap. 4 că densitatea unui PES fiind invariantă pe domeniul său suport, constituie un obiect, în cazul de mai sus un obiect din clasa S₁. Acest PES are ca suport intervalul  de mărime , cu referinţa internă la x_k (referinţă dreapta, adică intervalul suport se află la stânga acestei valori). Aceeaşi valoare x_k poate fi însă referinţă internă şi pentru intervalul suport de aceeaşi mărime, dar aflat la dreapta referinţei x_k, , interval suport al unui alt PES cu densitatea:

                                                     (X.3.2.3.4)

 

Observăm că în abordarea obiectuală prin distribuţii, valoarea x_k (aceeaşi cu cea din abordarea clasică de mai înainte) devine o referinţă internă pentru două obiecte de tip interval (stânga şi dreapta), intervale ce constituie suportul a două variaţii uniforme de mărime  şi ,  aşadar x_k va fi referinţă internă şi pentru aceste procese, şi pentru densităţile acestora (distribuite uniform pe cele două intervale suport cu referinţa x_k).

Comentariul X.3.2.3.1: Faptul că două obiecte abstracte au aceeaşi referinţă internă nu înseamnă întotdeauna că cele două obiecte sunt unul şi acelaşi. Obiectul abstract stare S₀ cu referinţa x_k este distribuit pe intervalul de nedeterminare al PD respectiv, în timp ce obiectul abstract S₁ cu referinţa la x_k este distribuit pe un interval finit ce cuprinde mai multe valori singulare cunoscute (pentru a putea exista un proces nenul). în ambele cazuri x_k este acelaşi, dar mărimea domeniilor interne pe care le referă sunt diferite. Dacă aţi citit cap. 3 şi 4 în care erau specificate elementele componente ale unui obiect şi ale unui proces, reiese clar că obiectele din clasa S₀ şi cele din clasa S₁ nu pot fi confundate chiar dacă au aceeaşi referinţă internă. în cap. 4 s-a făcut clar precizarea că obiectele S₀ sunt stări ale unor obiecte (cu procese nule) iar obiectele S₁ sunt stări ale unor procese uniforme P₁).

Densitatea variaţiei totale (considerată şi ea uniformă) pe intervalul suport  (adunând şi scăzând la numărător pe f(x_k)) rezultă a fi:

                  (X.3.2.3.5)

 

de unde se obsevă că această densitate este egală cu valoarea medie a celor două densităţi stânga-dreapta cu referinţa la x_k. Faţă de această densitate medie (care este egală cu densitatea tangentei în P_k), considerată componentă comună a celor două densităţi (referinţă internă de clasă), vom avea cele două componente specifice ale densităţilor (date de funcţia D() introdusă în cap. 3):

                                                     (X.3.2.3.6)

 

componenta specifică a densităţii la stânga referinţei x_k şi:

                                                     (X.3.2.3.7)

 

componenta specifică a densităţii la dreapta aceleiaşi referinţe. Am văzut în cap. 4 când am discutat despre două PES concatenate (cum sunt şi variaţiile noastre) că pentru o relaţie de dependenţă neliniară aşa cum este f(x) cele două componente specifice ale PES trebuie să existe (să fie diferite de zero), altfel relaţia f(x) este o dreaptă (cazul tangentei).

în urma acestei analize obiectuale a obiectelor şi proceselor implicate în definirea noţiunii de derivată de ordinul I, putem face următoarele observaţii:

1)        Obiectul abstract "valoare singulară a unei variabile dependente y_k atribuită printr-o relaţie f unei valori singulare independente invariante x_k", constituie un obiect din clasa procesuală S₀ (clasă specifică obiectelor cu procese nule).

2)        Obiectul abstract "variaţie finită de ordinul I  a atributului y distribuită uniform pe o variaţie finită suport de acelaşi ordin " (unde x_k este referinţa internă a intervalului suport), constituie un PES din clasa P₁ (o diferenţă finită între două stări S₀); densitatea uniformă a acestui PES este o stare de proces din clasa S₁.

3)        Două variaţii , cu intervale suport egale ca mărime , simetrice faţă de o referinţă comună x_k vor constitui două PES concatenate, la care starea finală a primului este stare iniţială a celui de-al doilea, această stare comună (de tip S₀) fiind în cazul din fig. X.3.2.3.1 punctul . Aceste PES, fiecare în parte, pot avea domenii suport oricât de mici dar cu condiţia ca suportul să conţină mai mult de o valoare singulară cunoscută (pentru a putea exista o variaţie liniară ), aşa că ele nu pot converge niciodată spre un punct, fie el şi punct dimensional.

Cu acest din urmă amendament, putem păstra notaţia pentru intervalele infinitesimale din calculul diferenţial, variaţiile  şi  devenind dy şi dx, care vor putea avea ca referinţă internă o valoare singulară, dar nu vor putea niciodată să fie înlocuite de o valoare singulară (un singur punct). în aceste condiţii, relaţiile X.3.2.2.3 şi X.3.2.2.4 rămân în continuare valabile şi în matematica bazată pe distribuţii, dar derivata de ordinul I nu mai este limita (asimptota) spre care tinde raportul variaţiilor, ci densitatea unui PES de ordinul I. O altă precizare importantă, domeniul dx în cazul proceselor realizabile (al calculelor numerice) nu poate fi mai mic decât , intervalul de eroare cu care pot fi reprezentate valorile numerice concrete pe SPI efector. în cazul PES concatenate la care intervalul suport  nu poate fi neglijat (neglijare impusă de actualele formule de obţinere a derivatelor funcţiilor, valabile pentru ), pentru calculul densităţilor distribuţiilor nu se poate folosi decât calculul cu diferenţe finite.