X.3.6.1 Modelul punctului cu dimensiuni

Am văzut în cap. 3 că un obiect înseamnă o distribuţie a cel puţin unei proprietăţi pe un domeniu suport, distribuţie invariantă, evaluată faţă de un sistem de referinţă intern. Pentru a putea deosebi (discerne) între ele două sau mai multe obiecte existente simultan, respectivele  obiecte trebuie să difere prin cel puţin un atribut diferenţial (vezi condiţiile 3.1.a ...d din par. 3.1). Am văzut de asemenea că un punct realizabil înseamnă o valoare numerică trunchiată (numită în această lucrare valoare normală), iar un punct virtual, o VAE. Privit ca un obiect elementar (un element de distribuţie), punctul realizabil are ca domeniu suport un interval finit (intervalul de nedeterminare, de incertitudine, de eroare etc.) pe care este distribuit uniform atributul său existenţial, iar punctul virtual are ca suport o singură VAE din {R} cu atributul său existenţial, adică o distribuţie Dirac virtuală, cu un interval de nedeterminare nul.

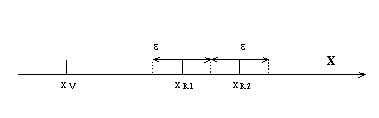
Fig. X.3.6.1.1

în fig. X.3.6.1.1 avem o reprezentare grafică a celor două cazuri, axa X fiind o reprezentare pentru axa numerelor reale {R}. în această reprezentare, x_V corespunde unei valori singulare virtuale (o distribuţie Dirac cu referinţa internă la VAE x_V), iar x_R1 şi x_R2, fiecare cu intervalul de nedeterminare  corespund la două valori realizabile. Reamintim că mărimea lui  este dată de relaţia:

                                                                                                        (X.3.6.1.1)

identică cu X.3.1.1.2, unde  este mărimea unui interval finit aparţinând axei X iar  este numărul de valori singulare distincte existente în acest interval. Mărimea , echivalentă cu o densitate (aşa cum am văzut în par. X.3.1.1) reprezintă numărul de valori singulare pe intervalul unitate de axă, număr care pentru mulţimea  realizabilă este întotdeauna finit.

Dacă revenim la valorile x_R1 şi x_R2 din fig. X.3.6.1.1, ele reprezintă aşa cum spuneam mai sus două valori normale, distribuţii uniforme a atributului existenţial pe domeniul suport , cu referinţe interne tot VAE dar de această dată realizabile printr-o convenţie specială de trunchiere. Deoarece orice interval trebuie definit ca mărime prin cele două frontiere cunoscute ale sale, în cazul valorilor singulare realizabile intervalul de nedeterminare este dat fie de diferenţa dintre două astfel de valori normale succesive, în cazul nostru , fie de o valoare impusă pentru numărul . Conform celor stabilite mai sus, x_V corespunde unui punct virtual iar  unui punct realizabil cu referinţa internă centrală.

Comentariul X.3.6.1.1: Este momentul unei explicaţii pentru o contradicţie evidentă apărută ca urmare a introducerii termenului de VAE realizabilă. Adică pe tot parcursul acestei lucrări se atrage atenţia asupra dihotomiei dintre obiectele abstracte realizabile şi obiectele virtuale, iar acum vorbim de obiecte virtuale realizabile. Ei bine nu este vorba de nicio contradicţie ci doar de o convenţie specială de trunchiere, convenţie ce permite reprezentarea doar pentru anumite valori numerice, a unor şiruri infinite de cifre folosind câteva reguli speciale de sintaxă. în matematici este bine cunoscută regula de notare pentru numerele zecimale cu grupuri de cifre ce se repetă identic de la o anumită poziţie după separatorul zecimal (aşa numitele perioade zecimale). De exemplu 1/3=0,(3) unde grupul de cifre (în exemplul nostru format dintr-o singură cifră) din paranteze este perioada. Această notaţie simbolizează că grupul din paranteze se repetă la infinit. Alte exemple: 1/6=0,1(6); 1/11=0,(09); 1/13=0,(076923) şi multe altele. Această convenţie de notare are un caz particular : când perioada zecimală este formată exclusiv din zerouri, nu se mai scrie nimic (de exemplu 1,(0)=1; 1/4=0,25(0)=0,25 etc.). Vom numi valorile numerice obţinute prin această ultimă convenţie de reprezentare valori relativ exacte (VRE) deoarece sunt dependente de o convenţie de trunchiere (a şirului de zerouri). Aşadar dacă avem o VAE care constă dintr-un număr finit de cifre după care urmează un şir infinit de zerouri, renunţarea la acel şir de zerouri face reprezentarea realizabilă. Este însă doar o convenţie de reprezentare de care trebuie ţinut cont - valoarea din {R} ce corespunde respectivei valori trunchiate conţine o infinitate de cifre (de zerouri). Aşa stau lucrurile de exemplu în ce priveşte numerele întregi; dacă ar fi să le reprezentăm corect din p.d.v. informaţional ca tăieturi ale mulţimii {R} la intervale unitate, după fiecare reprezentare numerică a acestora ar trebui să urmeze separatorul zecimal urmat de un şir infinit de zerouri. Convenţia tacită de reprezentare doar a cifrelor diferite de zero din faţa separatorului zecimal rămâne totuşi o formă de trunchiere.

Să revenim la modelul punctului din fig. X.3.6.1.1 în varianta punctului realizabil. în acest caz avem tot o singură valoare cunoscută - referinţa internă x_Rk - la care se asociază intervalul de nedeterminare e, dar de această dată valoarea x_Rk este o VRE (aşa cum spuneam mai sus, un tip special de VAE ce poate fi reprezentată prin renunţarea la un şir infinit de zerouri).

Valoarea de referinţă internă a punctului realizabil poate avea diferite poziţii în interiorul domeniului intern , dintre acestea cele mai cunoscute fiind trei: poziţia de extremă stânga, de extremă dreapta şi centrală. în fig. X.3.6.1.1 este reprezentată varianta cu referinţă centrală, caz în care domeniul  se divide în două subdomenii egale de o parte şi alta a referinţei. Frontiera inferioară a domeniului va fi la , cea superioară la , iar folosind notaţia pentru intervale deschise din matematici, acest domeniu se poate scrie . în cazul referinţelor stânga sau dreapta utilizăm notaţia pentru intervale semideschise, fiind foarte convenabilă în cazul concatenării punctelor realizabile. în varianta cu referinţa de extremă stângă, intervalul suport se poate scrie , iar în varianta de extremă dreaptă .

Pentru obiectul punct realizabil, aşa cum menţionam şi în cap.2, filosofia obiectuală propune o denumire specială şi anume: punct dimensional (PD). în cazul unui domeniu monodimensional (1D) al unui atribut calitativ X, modelul acestui obiect abstract poate fi definit ca:

1)    Domeniu interior, intervalul de trunchiere (nedeterminare, incertitudine)  asociat  unei VAE x_R din mulţimea {R}, interval în care nu mai este cunoscută nicio altă valoare intermediară şi pe care este distribuit uniform atributul existenţial al PD;

2)    Referinţa internă a obiectului PD este respectiva VAE, în urma procesului de trunchiere devenită o VRE reprezentabilă cu un număr finit de cifre;

3)    Frontierele obiectului sunt cele două valori x_s (frontiera superioară) şi x_i (frontiera inferioară) cu valori obţinute prin relaţii dependente de convenţia de poziţionare a referinţei interne, relaţii menţionate mai sus.

Folosind sintaxa matematică literală pentru intervale de valori numerice semideschise, obiectul PD 1D poate fi reprezentat în varianta referinţei de extremă stângă astfel:

           (X.3.6.1.2)