Anexa X.6 - CLASE PROCESUALE DE OBIECTE

 

Pentru o înţelegere mai uşoară a noţiunii de obiect procesual vom analiza existenţa unor astfel de obiecte în cazul foarte cunoscut al proceselor de mişcare. După parcurgerea acestei anexe, cititorul va putea apoi să înţeleagă că obiecte procesuale pot exista în cadrul oricăror procese, indiferent de atributul variabil şi indiferent de suportul distribuţiei ce descrie procesul.

Mişcarea de translaţie a unui SM este un proces specific de variaţie a unui atribut - vectorul de poziţie spaţială - al referinţei interne T a SM, faţă de o referinţă externă. Analiza obiectual-procesuală a proceselor de mişcare pune în evidenţă posibila existenţă a mai multor tipuri de procese elementare specifice (PES de tip P₀, P₁, P₂ etc.) şi a mai multor tipuri de stări ale acestor PES de mişcare (S₀, S₁, S₂ etc). Toate obiectele de tip stare de care vorbim sunt elemente ale unor distribuţii (cu suport temporal în cazul mişcării); stările S₀ sunt elemente ale unei distribuţii primare, stările S₁, S₂, S₃ sunt elemente ale distribuţiilor derivate de ordinul I, II respectiv III ale celei primare. Am văzut în cap. 5 că distribuţia temporală primară a poziţiilor spaţiale ale unui SM aflat în mişcare este o distribuţie Lagrange (o traiectorie):

                                                                                                                    (X.6.1)

 

O astfel de traiectorie realizabilă (obţinută în urma unui proces de eşantionare) este reprezentată în fig. X.6.1, într-un caz simplu cu doar cinci elemente într-un spaţiu 2D:

                                                                    (X.6.2)

 

suficiente pentru a explica concret compoziţia distribuţiilor derivate până la ordinul III.

 

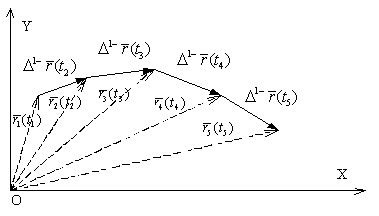
Fig. X.6.1

Elementele unei astfel de distribuţii sunt stări din clasa S₀ cu procese specifice nule (P₀), fiecare element având ca suport (în cazul unei distribuţii realizabile) un PD temporal (o valoare normală de pe axa timpului).

Aşadar momentele t₁ ...t₅ sunt PD temporale la care au fost prelevate eşantioane ale poziţiei spaţiale a SM în mişcare, momente ce satisfac următoarea condiţie: valorile t_k (k=[1,5]) sunt referinţe interne (dreapta[1]) ale unor PD temporale de mărime  dispuse la intervale egale  (deci diferenţele finite temporale de ordin mai mare ca unu sunt nule).

Mişcarea este presupusă atât de neuniformă încât există diferenţe finite ale vectorului de poziţie până la ordinul trei (pentru a exista procese până la acest ordin). în cazul existenţei mişcării, condiţia de stare S₀ impune ca mărimea PD temporal suport (durata unui eşantion) să fie suficient de mică pentru ca procesul de mişcare să poată fi considerat neglijabil (adică nul).

Un PES de mişcare de ordinul I (P₁) constă dintr-o variaţie de poziţie liniară şi finită , distribuită pe un domeniu suport  (între două stări de tip S₀, vezi fig. X.6.1).

Comentariul X.6.1: Reamintim cititorului că simbolul  sau  reprezintă o diferenţă finită dreapta (anterioară), respectiv stânga (posterioară) faţă de elementul referinţă  dintr-un şir ordonat de n valori singulare ale variabilei . în cazul unei diferenţe finite de ordinul I vom avea:

 

                                                                                                           (X.6.3)

 

                                                                                                           (X.6.4)

 

S-a folosit o astfel de notaţie, cu poziţia semnului inversată, pentru a nu se confunda ordinul unei diferenţe finite cu un exponent (o putere).

Mărimea intervalului  (perioada de eşantionare) se alege astfel încât să poată exista variaţie de poziţie, dar această variaţie să poată fi considerată liniară (cu densitate uniformă).

Starea de tip S₁ (densitatea temporală a variaţiei liniare a poziţiei, viteza) a PES de ordinul I, uniform distribuită pe intervalul suport este:

                                                                              (X.6.5)

 

 

adică densitatea unui element de distribuţie derivată de ordinul I:

 

                                                                                                               (X.6.6)

 

a distribuţiei primare X.6.2.

 

Comentariul X.6.2: Se observă că avem un raport dintre o mărime vectorială (diferenţa de ordinul I a doi vectori) şi un scalar (un interval temporal), fapt din care rezultă că densitatea distribuţiei respective este o mărime vectorială. Cititorul este invitat să accepte că densităţile distribuţiilor sunt scalari doar în cazul distribuţiilor primare, unde atributul distribuit este şi el scalar, iar dacă atributul distribuit este o mărime vectorială (un proces, cazul distribuţiilor derivate), atunci şi densitatea va fi un vector. în cazul unei densităţi vectoriale invariante (pe domeniul său suport) acest lucru implică invarianţa simultană a modulului şi direcţiei acesteia.

 

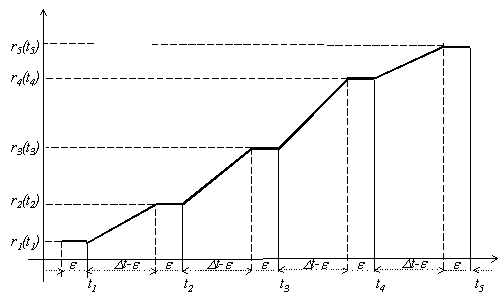
Fig. X.6.2

în fig. X.6.2 este reprezentată evoluţia în timp a informaţiei[2] despre modulul vectorului de poziţie, pentru a putea evidenţia clar care sunt intervalele suport ale celor două tipuri de stări S₀ şi S₁. în intervalele de eşantionare cu mărime   (mărimea unui PD) am stabilit că vectorul de poziţie rămâne invariant, iar în intervalul ce corespunde perioadei de eşantionare (), vectorul de poziţie este liniar variabil. Din fig. X.6.2 se observă că de fapt intervalul suport al mişcării este  şi nu aşa cum indică relaţiile X.6.5 şi X.6.7, deoarece pe intervalul  mişcarea este nulă (poziţie invariantă prin definiţia stării S₀). Pentru a nu complica prea tare relaţiile, am renunţat la menţionarea lui  în relaţiile X.6.5 şi X.6.7, dar cititorul trebuie să ţină cont de aceste precizări pentru a înţelege clar că suportul temporal al stării  (stare S₀) este diferit de suportul stării  (stare S₁), cele două intervale temporale fiind adiacente dar disjuncte.

Cu toate că referinţa temporală a ambelor obiecte este aceeaşi valoare t_k, în cazul stării S₀ ea este o referinţă internă inclusă în intervalul suport, în timp ce în cazul stării S₁ ea este o referinţă asimptotică (este adiacentă, dar nu face parte din intervalul suport). în limbaj matematic, folosind notaţia pentru intervale închise şi deschise, intervalul suport al stării  este , în timp ce intervalul suport al stării  este . Din fig. X.6.2 rezultă clar că poziţia şi viteza unui obiect material nu pot fi cu existenţă simultană, cu toate că ambele obiecte abstracte au aceeaşi valoare de referinţă t_k.

Pentru PES de mişcare de ordinul II, starea de tip S₂ (densitatea temporală a variaţiei uniforme a vitezei, acceleraţia) uniform distribuită pe intervalul suport Dt este:

      (X.6.7)

 

adică densitatea unui element de distribuţie derivată de ordinul II:

                                                                                                             (X.6.8)

 

în cazul concret al distribuţiei primare X.6.2, distribuţia derivată de ordinul II va fi:

                                                                                 (X.6.9)

 

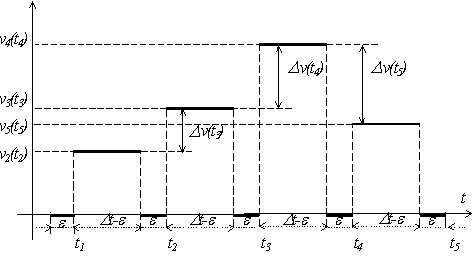
 Fig. X.6.3

în fig. X.6.3 este reprezentată distribuţia X.6.7 (numai modulele vitezelor), din care se pot vedea atât modulele vitezelor cât şi cele ale variaţiilor de viteză . Această reprezentare (dar şi cele din fig. X.6.1 sau X.6.2), trebuie înţeleasă în mod nuanţat. Cu linie îngroşată este reprezentată distribuţia temporală a informaţiei despre viteză pe care ne-o furnizează procesul de eşantionare, nu viteza reală a procesului de mişcare pe care îl studiem, dar această informaţie fragmentată este singura pe care o putem obţine, şi singura cu care putem opera în procesul de prelucrare a informaţiei.

 

Comentariul X.6.3: Cititorul trebuie să înţeleagă şi să facă distincţie între un proces real de mişcare şi o informaţie despre acel proces. Noi putem avea despre un obiect sau proces extern corpului nostru doar informaţii parţiale furnizate de organele noastre de simţ şi de alte mijloace ajutătoare, dar nu informaţia totală despre acel obiect sau proces, informaţie care este infinită cantitativ. Atât poziţia cât şi viteza sau acceleraţia unui obiect în mişcare sunt doar informaţii pe care noi le grupăm în anumite categorii pentru a le putea deosebi (discerne) unele de altele, informaţii care sunt unica noastră legătură dintre creierul nostru şi lumea exterioară. Când spunem că poziţia şi viteza nu pot fi cu existenţă simultană, ne referim în special la informaţia despre poziţie şi la informaţia despre viteză. Dar chiar idealizând informaţiile parţiale (reducând intervalele suport  şi  spre zero), tot nu putem să facem abstracţie de principiul noncontradicţiei (vezi anexa X.5) care interzice ca acelaşi atribut să fie şi constant şi nonconstant (variabil) în acelaşi interval de timp.

 

Din fig. X.6.3 vedem că informaţia despre variaţia vitezei apare cu întârziere de o perioadă de eşantionare, dar această variaţie există (este distribuită) pe aceeaşi durată cât există şi viteza, adică tot pe un interval .

Pentru PES de mişcare de ordinul III, starea de tip S₃ (densitatea temporală a variaţiei uniforme a acceleraţiei) distribuită pe intervalul suport este:

                                                   (X.6.10)

 

densitatea unui element de distribuţie derivată de ordinul III:

                                                                                                            (X.6.11)

 

a distribuţiei primare X.6.1.

 

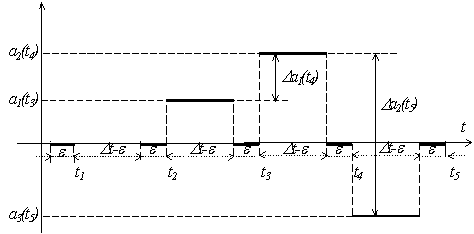
Fig. X.6.4

Din fig. X.6.4 în care este reprezentată distribuţia modulului acceleraţiei (modulele distribuţiei X.6.11), vedem că informaţia despre variaţia acceleraţiei apare cu o întârziere de două perioade de eşantionare.

 

Comentariul X.6.4: Stările procesuale S₁, S₂ şi S₃ despre care am discutat până acum şi care am ajuns la concluzia că sunt obiecte (abstracte evident), deoarece sunt distribuţii invariante pe domeniile lor suport, pe lângă faptul că sunt obiecte, mai sunt şi obiecte compuse. Din relaţiile lor de definiţie X.6.5, X.6.7 şi X.6.10 vedem că o stare S₁ are la bază (în compunere) o relaţie dintre două stări S₀, o stare S₂ este compusă din două stări S₁ sau din trei stări S₀ ş.a.m.d. Toate aceste componente ale unei stări sunt obiecte abstracte, care în momentul evaluării sunt operanzi ai unui proces abstract (de prelucrare a informaţiei, de calcul) executat de un SPI; dar aşa cum am văzut în cap. 8, operanzii unui anumit proces abstract trebuie să fie toţi cu existenţă simultană, în timp ce stările pe care ei le reprezintă nu mai există la momentul respectiv (au existat la momente anterioare). Pentru acest motiv, toate informaţiile privind stările anterioare percepute de SPI trebuiesc stocate, iar stocarea are loc într-o componentă fundamentală a unui SPI - memoria acestuia. Tot în cap.8 am văzut (axioma memoriei) că într-o memorie nu pot fi stocate decât obiecte (cantităţi invariante şi finite de informaţie). Acesta este motivul pentru care filosofia sistemică a recurs la abordarea obiectuală a cunoaşterii, abordare în unele cazuri mult diferită faţă de abordarea existentă astăzi, dar bazată pe faptul că nu se poate separa cunoaşterea de procesele abstracte din mintea umană sau din SAPI, iar aceste procese nu pot fi înţelese fără un model corect şi general al SPI, model care ne explică ce însemnă de fapt prelucrare de informaţie.

 

Pentru ca în încheiere cititorul să înţeleagă mai bine esenţa abordării obiectuale a mişcării, să ne imaginăm că tot acest proces pe care l-am analizat este un film de animaţie extrem de simplu format doar din cinci cadre, în care un punct de pe ecran (referinţa internă T a obiectului ce se mişcă) execută mişcarea de la poziţia  la . Fiecare cadru corespunde unei stări S₀ a obiectului punctual (în orice film un cadru este o asemenea stare a tuturor obiectelor surprinse în cadru, toate stau nemişcate deoarece au fost imprimate, (memorate), cadrul având ca suport temporal intervalul e (care la filmare corespunde timpului de expunere iar la redare timpului de iluminare al respectivului cadru). între două cadre există un interval finit (câteva PD temporale), suficient de mare pentru ca la o viteză dată a procesului de mişcare, între două cadre să apară diferenţe de poziţie sesizabile ale obiectelor.

Acest interval  este suportul temporal al procesului uniform P₁ iar densitatea sa (invariantă pe acest interval) este viteza constantă de mişcare (presupusă constantă doar în acest interval), o stare S₁. în cazul unui film, acest interval este folosit la avansul peliculei cu un cadru (deci la un proces de mişcare ce substituie mişcarea obiectului filmat). Pentru că şi creierul uman funcţionează similar (tot prin eşantionare şi memorare), pentru el este foarte uşor să "sintetizeze", să reconstituie mişcarea din cadrele (eşantioanele) prezentate ca şi cum această mişcare ar fi continuă. în final, obişnuitele observaţii:

1)      Obiectele S₀ cu procese specifice nule (P₀) există (pentru un SPI) pe durata intervalului lor suport, un PD temporal (în cazul proceselor de mişcare, dar dacă obiectul nu se mişcă starea S₀ poate dura nelimitat). Procesele P₁ există la rândul lor tot pe durata suportului lor temporal, adică o mulţime de PD concatenate ce formează un interval finit de ordinul I, cu o astfel de mărime încât procesul să poată fi considerat uniform. Cele două domenii temporale (un PD pentru obiectul S₀ şi o mulţime de PD pentru obiectul S₁) sunt diferite, aşadar obiectele S₀ şi S₁ nu sunt cu existenţă simultană. Acelaşi atribut - poziţia spaţială - nu poate fi şi invariant (P₀) şi variabil (P₁) simultan. Cele două obiecte abstracte - unul o stare a unui obiect (S₀) şi celălalt o stare a unui proces (S₁) - au domenii suport diferite, deci nu pot exista la acelaşi moment şi poziţie determinată şi viteză determinată.

2)      Abordarea obiectuală specifică acestei lucrări, bazată pe distribuţii, relevă astfel o eroare fundamentală a fizicii clasice - acceptarea existenţei simultane a poziţiei şi impulsului (vitezei) unui SM. Această eroare derivă de la o altă eroare de această dată din matematici - existenţa derivatei într-un punct singular - eroare de aceeaşi factură, ce poate fi şi ea observată dacă analizăm obiectual noţiunea de derivată prin prisma noţiunilor specifice filosofiei obiectuale (vezi anexa X.3).

3)      Definirea proceselor elementare specifice (PES) ca distribuţii temporale cu densitate uniformă  ale unor variaţii (diferenţe finite de ordinul I dintre două stări S_x), permite pe de o parte analiza proceselor oricât de complexe prin descompunerea lor în PES de diferite ordine, şi pe de altă parte, înţelegerea mai clară a operaţiilor cu obiectele abstracte substitut  pentru PES - vectorii.

4)      Clasele de obiecte procesuale conţin obiecte abstracte definite prin procese elementare (adică numai prin procese uniforme). în cazul obiectelor reale, ce sunt supuse proceselor reale, aceste clase de obiecte procesuale (existente doar în memoria unui SPI) au asociat întotdeauna ca atribut de model un interval temporal ce poate fi considerat ca o "istorie" a obiectului respectiv. Utilizarea exclusivă a proceselor uniforme ca procese elementare este datorată proprietăţii acestora de a nu conţine informaţie diferenţială internă (în intervalul temporal suport densitatea variaţiei este uniformă, aşadar nu există elemente de contrast intern ale densităţii).