4.5 Procese elementare specifice concatenate

Am văzut că un PES (reprezentat de un vector) este un proces uniform, de variaţie definită a unui atribut de stare, între două valori - starea iniţială şi cea finală. Dacă starea finală a unui proces PES₁ (S₀₂ în fig.4.5.1) devine stare iniţială pentru un alt proces PES₂ atunci spunem că cele două procese sunt concatenate (înlănţuite, în cazul proceselor cu suport temporal, PES succesive). Acest proces abstract de concatenare poate continua oricât de mult, astfel putându-se reprezenta procese specifice şi individuale de orice fel, în aceeaşi manieră precum orice distribuţie, oricât de complicată, se poate descompune în distribuţii elementare uniforme.

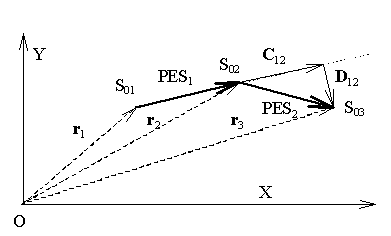
Fig. 4.5.1

în fig. 4.5.1 sunt reprezentate două astfel de PES concatenate PES₁ şi PES₂, care au conform relaţiilor 4.4.5 şi 4.4.7 componenta comună C₁₂ = C(PES₁, PES₂) şi componenta specifică (a lui PES₂ faţă de PES₁) D₁₂ = D(C₁₂, PES₂) evaluate faţă de aceeaşi direcţie de referinţă a PES anterior. Componenta comună are aceeaşi direcţie cu direcţia de referinţă iar componenta specifică are direcţia perpendiculară pe direcţia de referinţă.

Observăm că două PES succesive vor avea aceeaşi direcţie dacă între cele două PES nu există nicio componentă specifică (normală pe direcţia comună).

Comentariul 4.5.1: Introducerea noţiunilor de componentă comună şi specifică a două PES concurente şi a relaţiilor de definire a acestora, oferă nişte posibilităţi noi de a defini noţiuni greu sau impropriu definite până acum. Una dintre acestea este de exemplu definiţia dreptei. în manualele de matematici elementare definiţia frecventă a acestui obiect abstract este următoarea: "Linia dreaptă este drumul cel mai scurt dintre două puncte". Acest mod de a defini o dreaptă enunţă o proprietate optimală a dreptei (ca rezultat al unei alegeri dintre toate drumurile posibile intre cele două puncte) dar nu şi procesul de generare a unui asemenea obiect. Utilizarea noţiunilor de componentă comună şi diferenţială a două PES, aplicabilă şi pentru procese concatenate, permite o definiţie procesuală a dreptei: "Un şir de PES de ordinul I concatenate, la care componenta specifică a două PES adiacente este invariant nulă este reprezentat de o dreaptă".

Cauza apariţiei componentelor diferenţiale într-un şir de PES concatenate o vom afla în capitolele sau anexele următoare. Deocamdată vedem că absenţa unei astfel de componente duce la un proces uniform cu aceeaşi direcţie, reprezentat în sintaxa vizual-grafică de o linie dreaptă, aşa cum menţionam mai sus. Acest fapt justifică reprezentările sub formă de drepte (axe) a mulţimilor continue de valori ale unui atribut monodimensional (este evident, deoarece existând o singură dimensiune nu poate exista componentă diferenţială a direcţiei între două variaţii succesive), dar tot acest fapt este justificarea fundamentală a mişcării după o traiectorie rectilinie a sistemelor materiale ce nu sunt supuse acţiunii unor forţe cu componentă normală pe traiectorie,  situaţie cu un caz particular - absenţa acţiunii oricărei forţe - ce corespunde mişcării unui SM izolat cu viteză iniţială.