Anexa X.20 – REFERINŢE INTERNE NATURALE

Fie o distribuţie spaţială 3D, uniformă, finită şi invariantă a unui atribut, de exemplu densitatea masică . Faţă de o referinţă externă X, Y, Z, fiecare PD_i a distribuţiei (elementul de distribuţie primară) are vectorul de poziţie , conform fig. X.20.1.

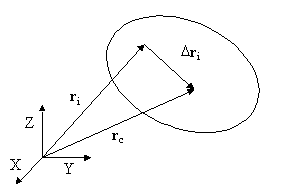
Fig. X.20.1

Componenta comună a mulţimii vectorilor de poziţie este tot un vector de poziţie, pe care să-l notăm . Faţă de acest vector unic şi invariant (ca poziţie internă) al distribuţiei, fiecare vector de poziţie  are o componentă diferenţială (specifică) . Dacă prin convenţie stabilim pentru mulţimea elementelor distribuţiei următoarea regulă: componenta comună a mulţimii componentelor specifice este nulă (inexistentă), atunci această condiţie transpusă în cazul din fig. X.20.1 devine:

                                                                                               (X.20.1)

care scrisă pe componente înseamnă:

                           , ,                      (X.20.2)

Dacă presupunem că distribuţia 3D conţine n elemente, adică i=[1,n], atunci relaţiile X.20.2 mai pot fi scrise:

                                      , ,                                (X.20.3)

de unde rezultă:

                                   , ,                             (X.20.4)

cunoscutele relaţii ce definesc coordonatele centrului de masă (sau de greutate) ale unui obiect material cu distribuţie uniformă a densităţii masice.

Rezultă că poziţia centrului reprezintă componenta comună a poziţiilor spaţiale ale mulţimii elementelor de distribuţie, obiect abstract ce reprezintă în acelaşi timp o referinţă naturală internă T a respectivei distribuţii (faţă de care se estimează componentele specifice ale fiecărui element). Relaţiile X.20.4 sunt valabile pentru orice distribuţie discretă, cum ar fi de exemplu şiruri finite de valori numerice; în acest caz, componenta comună (referinţa internă naturală) a acestor şiruri este valoarea medie aritmetică. De asemenea, relaţiile X.20.4 justifică relaţia X.20.1 (pe care am folosit-o înainte de a o justifica), din care se obsrvă că valoarea componentei comune este nulă dacă suma valorilor individuale (specifice) este nulă (afirmaţie valabilă pentru atribute cantitative).

Comentariul X.20.1: Trebuie subliniat faptul că atât componenta comună a unei mulţimi de obiecte cât şi celelalte valori de referinţă, fie naturale, fie artificiale, sunt obiecte abstracte fără nicio corespondenţă în obiectele mulţimii pe care se face evaluarea lor (sunt referinţe externe acestor obiecte). Dacă ne referim la mulţimea vectorilor din fig. X.20.1, este un vector de poziţie al unui punct imaginar (nu există vreun element al distribuţiei la acea poziţie decât din pură întâmplare).