Anexa X.8 - MĂRIMI VECTORIALE LOCALE ŞI GLOBALE

 

în această anexă sunt prezentate pentru reamintire cele mai frecvent întâlnite relaţii din teoria câmpurilor vectoriale care sunt utilizate pe parcursul lucrării, cu menţiunea că denumirile noţiunilor sunt cele din matematici, unele din acestea fiind redefinite în acestă lucrare.

1)      Gradientul unui câmp scalar r(x,y,z) este un vector  dat de relaţia:

                                                                                             (X.8.1)

 

unde sunt versorii axelor X, Y, Z.

2)      Flux elementar al vectorului  se numeşte produsul , unde  este elementul de arie orientat (). Dacă elementul de arie înconjoară un punct P(x, y, z), atunci vom avea fluxul elementar în P.

3)      Flux total (global) al vectorului  printr-o suprafaţă oarecare  este:

                                                                                                                  (X.8.2)

 

4)      Fluxul total  printr-o suprafaţă închisă  care mărgineşte un volum  se mai numeşte productivitatea volumului . Raportul  este productivitatea medie a unităţii de volum, iar limita acestui raport când toate punctele suprafeţei  tind spre un punct interior P se numeşte divergenţa câmpului vectorial V în punctul P:

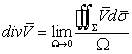                                                                                                    (X.8.3)

 

în ipoteza că derivatele parţiale ale lui  sunt continue în P, limita există şi poate fi exprimată prin:

                                                         (X.8.4)

 

5)        Rotorul unui câmp vectorial ,  , se defineşte folosind circulaţia  pe o curbă închisă C. Prin punctul P se duce un plan având versorul normalei . O curbă închisă C care înconjoară punctul P, situat în acest plan delimitează o arie . Se arată că limita raportului   când toate punctele curbei C tind către P este proiecţia unui vector pe direcţia , vector care se numeşte rotorul câmpului  în punctul P. Aşadar,

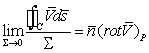                                                                                                (X.8.5)

unde

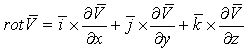                                                                       (X.8.6)

 

Circulaţia pe curba C se ia în sens direct faţă de  (regula şurubului drept). Rotorul mai poate fi scris sub forma unui determinant simbolic:

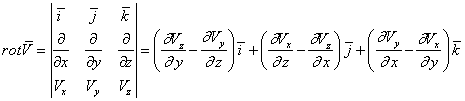                 (X.8.7)

 

 

 

6)        Formula integrală a divergenţei (Gauss-Ostrogradski):

                                                                                                  (X.8.8)

 

unde  este suprafaţa închisă ce mărgineşte volumul . Sensul normalei la suprafaţa orientată  este considerat pozitiv spre exterior . Din relaţia X.8.8 derivă alte două relaţii, formula integrală a rotorului:

                                                                                                (X.8.9)

 

care se mai poate scrie:

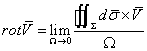                                                                                               (X.8.10)

şi formula integrală a gradientului:

                                                                                               (X.8.11)

 

7)        Formula lui Stokes:

                                                                                                   (X.8.12)

 

unde   este orice suprafaţă mărginită de curba închisă C .