7.6.6.4 Acţiunea energetică globală

în paragraful precedent am văzut în ce constă acţiunea unei cuante de flux energetic, proces cu două etape distincte, disjuncte dar adiacente temporal – incidenţa şi reflexia. în continuare, să analizăm procesul de acţiune al unor fluxuri energetice formate dintr-un mare număr de cuante atât ca arie efectivă, cât şi din p.d.v. al stocului energetic transportat. Am văzut că fluxul este o distribuţie spaţio-temporală a unui proces de transfer, aşa că toate procesele cuantice ale fluxului vor fi şi ele distribuite spaţio-temporal. Acest fapt înseamnă că procesele cuantice tratate în paragraful precedent se pot suprapune şi cumula aleator, dând impresia de continuitate a procesului. Ca urmare, cu toate că la nivel cuantic procesele de incidenţă şi reflexie sunt succesive, la nivel global de distribuţie cu număr foarte mare de elemente, aceste două procese ne par simultane, deoarece nu există o coerenţă temporală între intervalele suport cuantice. Este cazul fluxurilor din mediile L sau G, între ale căror elemente sunt relaţii de tip L sau G (pe care le-am discutat în cap. 5 şi 6). în cazul mediilor S, în care există relaţii rigide între toate elementele fluxului, cele două procese – incidenţa şi reflexia – pot fi succesive, la fel ca şi în cazul cuantic (cazul ciocnirilor elastice). Cu aceste precizări, să analizăm procesul general de acţiune energetică a unui FE asupra unui SM.

Să presupunem că avem un corp material SM_k aflat în repaos faţă de un sistem de referinţă extern SR_e, vectorul de poziţie al corpului faţă de această referinţă fiind , invariant[1]. Starea spaţială a SM_k este în acest caz o stare S₀ atât timp cât corpul rămâne nemişcat. O schimbare de stare spaţială a acestui corp înseamnă o variaţie a atributului poziţie spaţială - vectorul . Dar o astfel de variaţie înseamnă mişcare (de translaţie în acest caz), proces ce implică o viteză, iar apariţia unei viteze pornind din repaus înseamnă o variaţie a vitezei de la zero la o valoare oarecare, deci o acceleraţie.

în faza în care corpul era nemişcat, energia sa cinetică era nulă (faţă de SR_e), dar atât timp cât corpul se mişcă, energia sa este nenulă, aşadar pentru o schimbare de stare spaţială, corpul are nevoie de energie, care nu poate proveni decât din exteriorul său, de la un alt corp ce posedă energie transmisibilă, adică de la un flux energetic (FE) deschis. Am văzut în paragrafele anterioare că energia este o proprietate exclusiv transmisibilă, ea provenind de la un SM care o are (care se mişcă) şi care proprietate poate fi cedată printr-o interacţiune, altui corp material. Să analizăm lucrurile pentru început doar din partea corpului SM_k ce primeşte energie, corpul acţionat, reprezentat într-o secţiune parţială în fig. 7.6.6.4.1, pe suprafaţa sa reală de separaţie cuprinsă între cele două suprafeţe abstracte  (exterioară) şi  (interioară) existând un influx energetic exterior [2].

 

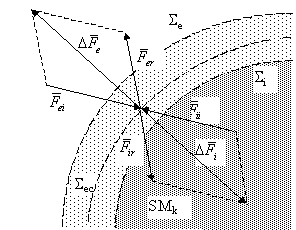
Fig. 7.6.6.4.1

La contactul dintre acest influx energetic şi SRS a SM_k va avea loc procesul de compunere dintre influxul exterior  şi influxul interior  (fluxul de reacţie, inerţial, relativ, vezi şi anexa X.7) al corpului acţionat, pe durata acestei compuneri suprafaţa de echilibru , a fluxurilor interactive fiind imobilă dacă fluxurile interactive sunt egale (starea de echilibru). în urma acestui proces, o parte din fluxul exterior va fi reflectat , va apărea astfel o variaţie a fluxului exterior  (reacţiunea fluxului intern), iar în interior, fluxul de reacţie, componentă a fluxului stocat intern, se va compune cu trafluxul extern, rezultând o variaţie a fluxului intern  (acţiunea fluxului extern). Pentru simplitate, neglijăm pe moment componentele tangenţiale ale fluxurilor, caz în care  şi  sunt colineare cu normala la suprafaţa de echilibru. în condiţii de echilibru ( imobilă faţă de SR_e), vom avea:

                                                                                                        (7.6.6.4.1)

 

adică variaţia fluxului exterior (reacţiunea) trebuie să fie egală şi de semn contrar cu variaţia fluxului interior (acţiunea). Dacă analizăm din p.d.v. strict vectorial fluxurile energetice externe din fig. 7.6.6.4.1, vedem că:

 

                                                                                  (7.6.6.4.2)

 

dar bilanţul influxului extern ne spune că la contactul cu SRS, el se divide în cele două părţi ale sale, fluxul extern transmis prin SRS (trafluxul extern) şi refluxul extern:

                                                                                                          (7.6.6.4.3)

 

Trafluxul extern va determina prin compunere cu fluxul intern preexistent, schimbarea de stare a sistemului acţionat. Din relaţiile 7.6.6.4.1 şi 7.6.6.4.3 rezultă:

                                                                                                                 (7.6.6.4.4)

 

şi corespunzător:

                                                                                                                 (7.6.6.4.5)

 

Relaţiile 7.6.6.4.4 şi 7.6.6.4.5 ne dau o informaţie foarte importantă, şi anume:

 Variaţia unui FE incident pe SRS a unui SM este egală şi de sens contrar cu fracţiunea din FE transmisă prin SRS.

Afirmaţia de mai sus este valabilă atât pentru FE externe cât şi pentru FE interne, stocate în interiorul SRS. Această variaţie a unui FE la contactul cu o SRS are în filosofia obiectuală un nume cunoscut.

 

 

Comentariul 7.6.6.4.1: Definiţia 7.6.6.4.1 stabileşte că forţa este un FE (variaţia unui flux este tot un flux), dar un tip special de flux, ce apare exclusiv la contactul unui FE cu SRS a unui SM. Cu alte cuvinte, dacă nu există o SRS cu a sa permeabilitate subunitară, şi un flux energetic stocat în interiorul său, ce ambele duc la apariţia unui flux reflectat, nu poate exista nici forţă. Pe baza relaţiilor 7.6.6.4.4 şi 7.6.6.4.5 mai observăm că forţa reprezintă în acelaşi timp şi un FE transmis printr-o SRS, dar numai în prezenţa celorlalte componente – fluxul incident şi cel reflectat. Cititorul va remarca poate că definiţia 7.6.6.4.1 este o definiţie independentă de definiţia newtoniană (inerţială) a forţei (F=ma), şi spre deosebire de această ultimă definiţie, definiţia 7.6.6.4.1 este valabilă în orice situaţie, inclusiv pentru forţele statice (pasive), pentru care definiţia newtoniană nu mai poate fi aplicată.

 

Ambele variaţii ale FE date de relaţiile 7.6.6.4.4 şi 7.6.6.4.5, egale şi de sens contrar, reprezintă cele două forţe egale şi de sens contrar, numite în fizica actuală forţa de acţiune şi forţa de reacţiune. Aceste variaţii se datorează compunerii pe SRS (mai exact în volumul de tranziţie al acesteia) a FE extern cu FE intern, compunere a componentelor omoloage, respectiv normale şi tangenţiale, până la momentul epuizării resurselor unuia din fluxuri.

 

Comentariul 7.6.6.4.2: Dacă un FE străbate o suprafaţă abstractă (de calcul, imaginară), transmitanţa acesteia fiind totală, nu poate exista flux reflectat, şi ca urmare nici nu poate apărea o forţă pe o astfel de suprafaţă.

 

Am văzut la (des)compunerea FE pe SRS că există câte două componente ale fluxurilor incidente, transmise şi reflectate, respectiv componentele normale şi cele tangenţiale. Ca urmare, şi variaţiile acestor fluxuri vor avea cele două componente, ceea ce face ca la impactul unui FE cu SRS să apară corespunzător două tipuri de forţe: forţa normală şi forţa tangenţială. De asemenea, am văzut că la incidenţa unui FE extern, toate componentele acestuia determină apariţia unor componente similare în interiorul SM, fluxurile de reacţie, ale căror componente normale şi tangenţiale vor determina apariţia forţelor de reacţie, tot cu cele două componente: normală şi tangenţială. Existenţa perechilor de forţe interactive este asigurată conform regulilor de compunere a FE, atâta timp cât fluxurile interactive dispun de resurse.

 

Comentariul 7.6.6.4.3: Existenţa componentelor normale şi tangenţiale ale forţelor în modelul SM propus de filosofia obiectuală permite o înţelegere clară şi coerentă a apariţiei forţelor de frecare. Se ştie din manualele de fizică de apariţia unei forţe de frecare atunci când două obiecte reale, aflate în contact, încearcă să se mişte unul faţă de celălalt. Forţa de frecare se opune mişcării de translaţie a obiecttelor, fiind proporţională (într-o primă aproximaţie) cu forţa de apăsare a obiectelor pe suprafeţele de contact, cu rugozitatea celor două suprafeţe, cu gradul lor de aderenţă şi dependentă de tipul de material al celor două obiecte. în abordarea obiectuală, forţa de frecare nu este altceva decât componenta tangenţială a forţei de reacţiune a mediului suprafeţei reale, forţă proporţională cu mărimea ariei transversale a SRS (rugozitatea celor două suprafeţe reale aflate în contact), cu presiunea de contact (nivelul energiei potenţiale barice din volumele de tranziţie ale celor două SRS), şi dependentă de proprietăţile fizico-chimice ale celor două medii aflate în volumul de tranziţie.

 

Până acum am discutat de forţele interactive în cazul egalităţii acestora, adică pe durata stării de echilibru, când suprafaţa de echilibru rămânea imobilă faţă de o referinţă externă. Să vedem ce se întâmplă în cazul unui dezechilibru, adică atunci când suprafaţa de echilibru se deplasează.

în fig. 7.6.6.4.2.a avem o secţiune printr-o incintă cilindrică al cărei volum este separat de un piston mobil în alte două volume V_a şi V_b presupuse egale. în cele două volume se află un acelaşi gaz, la aceeaşi temperatură şi presiune, rezultând că asupra pistonului se vor exercita forţele F_a şi F_b, egale şi cu sens opus. în aceste condiţii, pistonul va sta nemişcat, în volumul său fiind inclusă suprafaţa de echilibru dintre cele două forţe. în această stare, în cele două medii de tip G aflate în volumele V_a şi V_b sunt stocate aceleaşi stocuri de energie potenţială barică pV_a=pV_b (p fiind presiunea din cele două incinte) şi aceleaşi stocuri de energie potenţială termică nRT (unde n este acelaşi număr de moli de gaz din volumele V_a şi V_b, R constanta gazelor iar T temperatura absolută.

 

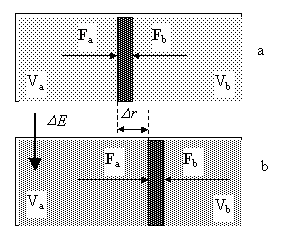
Fig. 7.6.6.4.2

Comentariul 7.6.6.4.4: Atenţie! Conform fizicii oficiale, în aceste condiţii de echilibru nu există transfer de energie între cele două medii din volumele V_a şi V_b ; conform filosofiei obiectuale, dimpotrivă, există transfer (flux) permanent de energie între cele două medii, dar cu intensităţi egale şi sensuri opuse, fluxuri ce sunt reprezentate de cele două forţe F_a şi F_b. Cum să nu existe FE atunci când moleculele de gaz se ciocnesc de suprafaţa pistonului şi apoi sunt reflectate? Variaţia impulsului acestora (cea care determină presiunea gazului) va produce întotdeuna o undă de şoc în mediul pistonului, undă ce va transfera energie dinspre gaz spre piston, iar reacţiunea pistonului (cea care produce reflexia moleculelor de gaz) însemnă transfer de energie de la piston spre gaz.

 

Să presupunem acum că în volumul V_a introducem o cantitate  de energie barică (un flux de gaz, vezi fig. 7.6.6.4.2.b), în urma acestui aflux de energie rezultînd în volumul V_a o creştere  a presiunii gazului. în urma acestui aflux, creşterea de presiune din V_a duce la mărirea forţei F_a, acum ea fiind mai mare decât F_b, ca urmare, pistomul (şi odată cu el suprafaţa de echilibru) se va deplasa comprimând gazul din V_b până când forţa de reacţiune F_b va fi din nou egală cu noua valoare a F_a. Deplasarea cu  a pistonului înseamnă o comprimare cu  a gazului din V_b, deci un aport de energie barică pentru gazul din acestă incintă. Iată că avem un caz de transfer de energie (flux energetic) de la mediul din V_a spre mediul din V_b, forţa F_a fiind de această dată o forţă activă, iar cantitatea  de energie barică transferată în acest proces constituind lucrul mecanic efectuat de forţa F_a.

 

 

Evident, lucrul mecanic efectuat de forţa F_a însemnă o pierdere pentru stocul energetic al obiectului agent (mediul din V_a) şi un câştig de energie pentru obiectul acţionat (mediul din V_b).

 

Comentariul 7.6.6.4.5: în acest exemplu am neglijat pentru simplitate atât procesele termice, cât şi masa pistonului, astfel încât să nu fim obligaţi să analizăm şi transformarea energiei potenţiale barice în energie cinetică a pistonului, pe parcursul mişcării sale, sau a energiei barice în energie termică şi invers. Definiţiile 7.6.6.4.3 şi 7.6.6.4.4 ne permit să identificăm ca forţe pasive atât forţele ce se opun unor forţe active (forţele de reacţiune) cât şi forţele aflate în echilibru (cazul din fig. 7.6.6.4.2.a).

 

Intensitatea unui FE transmis unui SM, adică densitatea temporală a procesului de transport energetic, intensitate care în termeni uzuali se numeşte putere, este dată de relaţia:

                                                                                                              (7.6.6.4.6)

 

unde  este cantitatea de energie ce traversează SRS a SM în intervalul . Dar aceeaşi intensitate a unui FE mai este dată de relaţia:

                                                                        (7.6.6.4.7)

 

unde  este VDF al FE, S este o suprafaţă abstractă de referinţă, este elementul orientat de arie al acesteia (fiind normala),  este densitatea de volum a energiei din FE agent, iar  este viteza de transfer a energiei prin .

 

Comentariul 7.6.6.4.6: Relaţia 7.6.6.4.7 este echivalentă cu relaţia 5.2.1.4 sau cu X.8.2; toate aceste relaţii ce exprimă intensitatea unui flux printr-o suprafaţă de referinţă sunt valabile numai pentru suprafeţe abstracte (teoretice, de calcul) şi nu pot fi aplicate suprafeţelor reale de separaţie. Aici intervin suprafeţele de echilibru, iar cititorul poate înţelege în sfârşit care este rostul acestora, şi anume, acela de suprafeţe de referinţă abstracte, pe care se pot aplica relaţiile de calcul ale intensităţilor fluxurilor interactive, suprafeţe aflate întotdeauna în interiorul volumului de tranziţie al suprafeţelor reale de separaţie.

 

Cum fluxurile interactive ce traversează SRS au cele două componente - normală şi tangenţială - rezultă că şi suprafaţa lor de echilibru va avea cele două componente - normală şi tangenţială. Pentru cazul FE printr-o SRS, relaţia 7.6.6.4.7 se poate scrie:

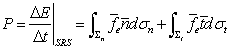                                                                      (7.6.6.4.8)

 

unde  şi  sunt componentele (proiecţiile) normală şi tangenţială ale suprafeţei de echilibru iar  şi  sunt elementele orientate de arie ale acestora.

în relaţia 7.6.6.4.8,  este VDF al FE ce traversează suprafaţa de referinţă, adică al unuia din fluxurile transmise prin SRS, respectiv  sau  din relaţiile 7.6.6.4.4 şi 7.6.6.4.5. Dar conform acestor relaţii:  şi , adică vectorii densitate de flux ale fluxurilor energetice transmise prin SRS sunt şi ei variaţiile VDF ale fluxurilor externe sau interne. Cu aceste precizări, putem scrie:

                                                                (7.6.6.4.9)

şi:

                                                              (7.6.6.4.10)

 

unde relaţia 7.6.6.4.9 exprimă puterea transmisă prin suprafaţa de echilibru de către forţa externă, iar relaţia 7.6.6.4.10 exprimă puterea transmisă prin aceeaşi suprafaţă de către forţa internă (de reacţiune), în condiţii de echilibru, adică atunci când suprafaţa de echilibru este imobilă.

Observăm că în toate aceste relaţii ce exprimă intensităţile unor FE sunt prezente împreună două atribute: o densitate de flux (VDF sau VQF) şi un element de suprafaţă orientat. Produsul lor scalar însemnă intensitatea unui FE elementar adică a unei forţe elementare. Cu alte cuvinte, intensitatea unei forţe elementare (o putere elementară) este dată de produsul dintre aria unui element de suprafaţă şi densitatea superficială a FE ce o traversează. Acestă densitate superficială a FE are în filosofia obiectuală un nume cunoscut.

 

 

Comentariul 7.6.6.4.7: Din definiţia 7.6.6.4.1 am văzut că variaţia pe SRS a unui FE este o forţă, iar din drfiniţia 7.6.6.4.5, presiunea rezultă a fi o densitate superficială a unei forţe. în literatura ştiinţifică actuală există relaţia F=pS, unde F, p şi S sunt toate mărimi scalare (F fiind modulul forţei, p presiunea şi S suprafaţa pe care presiunea este uniform distribuită). în filosofia obiectuală, presiunea fiind densitatea superficială a unui FE, adică a unui câmp vectorial, rezultă foarte clar că presiunea este o densitate de flux, deci un vector. Explicaţia pentru care în fizica actuală presiunea este o mărime scalară este scalarizarea mărimilor vectoriale (vezi anexa X.9), proces ce apare dacă mulţimea vectorilor succesivi ai unei distribuţii Lagrange sau mulţimea vectorilor simultani ai unei distribuţii Euler, nu au o componentă comună.

Referindu-ne la relaţiile 7.6.6.4.9 şi 7.6.6.4.10, vom avea:

                                                                                                            (7.6.6.4.11)

 

unde  este componenta normală a presiunii externe, iar:

                                                                                                              (7.6.6.4.12)

 

este componenta tangenţială a presiunii externe. La echilibru, acestora le vor corespunde în mod egal componenta normală a presiunii interne  şi componenta tangenţială a presiunii interne. în teoria câmpurilor vectoriale există relaţia Gauss-Ostrogradski (vezi anexa X.8), aplicabilă pentru fluxurile prin suprafeţe închise:

                                                                                      (7.6.6.4.13)

 

unde  este suprafaţa abstractă închisă a unui domeniu spaţial cu volumul V, traversată de fluxul vectorului . Acestă relaţie, în cazul fluxurilor energetice prin SRS, valabilă numai pentru componenta normală a presiunii, devine:

                                                                              (7.6.6.4.14)

 

de unde rezultă în general, pentru orice componentă normală a presiunii (internă sau externă) p_n, aplicată pe o SRS închisă a unui SM cu volumul V, relaţia:

                                                                                                           (7.6.6.4.15)

Comentariul 7.6.6.4.8: în relaţia 7.6.6.4.14 avem în partea stângă intensitatea unui FE printr-o suprafaţă închisă , iar în partea dreaptă un stoc energetic din volumul V, mai precis o variaţie de stoc intern din acest volum, ce corespunde unei anumite intensităţi de intrare sau ieşire prin , într-un interval . Acesta este sensul termenului de productivitate asociat divergenţei, termen cu o semnificaţie clară în cazul fluxurilor energetice. în cazul unui gaz închis în volumul V şi a unei distribuţii uniforme a presiunii, termenul din dreapta al relaţiei 7.6.6.4.14 devine pV, cunoscuta relaţie ce defineşte energia potenţială barică a gazului, energie ce nu poate apărea din senin, ci datorită unui proces generator, procesul de transport al acesteia, din exterior, prin suprafaţa .

 

O densitate de volum a unei mărimi distribuite într-un volum V, devine odată cu iniţierea  unei mişcări a distribuţiei, o densitate superficială a fluxului mărimii respective prin suprafaţa de referinţă  (vezi anexa X.15). în definiţia 7.6.6.4.5, am văzut că presiunea este o densitate superficială a unui FE prin suprafaţa de referinţă , de unde putem trage concluzia foarte importantă că, în cazul mediilor imobile, presiunea este densitatea de volum a energiei potenţiale barice stocate în volumul V, afirmaţie susţinută şi de membrul drept al relaţiei  7.6.6.4.14. Această energie este stocată într-un mediu atomic sau molecular aflat în volumul V, sub formă de flux stocastic, ale cărui elemente (VQF) sunt impulsurile individuale ale atomilor sau moleculelor, aflate în mişcare haotică.

 

Comentariul 7.6.6.4.9: Afirmaţia subliniată mai sus, verificată la nivelul singurelor medii cunoscute în prezent (mediile naturale: solide, lichide, gaze) este valabilă conform filosofiei obiectuale şi pentru celelalte generaţii de medii despre care am discutat în cap. 1 (mediile fundamentale proxime). Cu alte cuvinte, dacă într-un mediu există energie potenţială distribuită, atunci în mod clar trebuie să existe o presiune, iar unde există presiune şi un SM cu a lui SRS, va apărea şi o forţă dacă distribuţia spaţială de presiune este neuniformă.