2.2 Distribuţii virtuale

Noţiunea de distribuţie din matematică a fost introdusă ca o generalizare a conceptului de funcţie, astfel încât să se poată opera şi cu dependenţe între diferite variabile, ce nu puteau fi considerate funcţii din p.d.v. strict algebric (de exemplu dependenţele discontinue). Ca prime exemple de astfel de distribuţii discontinue, cu aplicaţii foarte largi, pot fi menţionate distribuţia Dirac  (numită şi funcţia impuls), distribuţia Heaviside  (numită şi funcţia treaptă) etc.

Pentru a înţelege distribuţiile trebuie înţeleasă mai întâi noţiunea de dependenţă dintre valorile a două mărimi.

 

Comentariul 2.2.1: Semnificaţia termenului foarte general de mărime folosit în matematici va putea fi înţeleasă mai bine de către cititor după parcurgerea întregii lucrări, mai ales a cap. 9. Singura precizare pe care o facem acum în avans este că un atribut (o proprietate a unui obiect real sau abstract) are conform filosofiei obiectuale două componente: componenta calitativă, reprezentată de numele sau simbolul proprietăţii respective (valoarea semantică a proprietăţii) şi componenta cantitativă, numită în această lucrare şi atribut existenţial, un număr (scalar) ce indică măsura (mărimea, cantitatea, gradul) existenţei respectivei proprietăţi. Aşa cum vom vedea mai încolo, în relaţiile din această lucrare, cele două componente sunt asociate conjunctiv, ceea ce înseamnă că pentru un obiect dat, ele nu pot exista decât împreună (o valoare nulă pentru atributul existenţial implică inexistenţa proprietăţii calitative asociate). în matematică, pentru a se asigura universalitatea limbajului, de cele mai multe ori se face abstracţie de atributul calitativ asociat, operându-se în majoritatea cazurilor numai cu atribute existenţiale (valori numerice) sau cu simboluri literale sau grafice pentru ele. în această lucrare, pentru a nu se pierde din vedere că pentru obiectele reale valorile numerice sunt totuşi atribuite unor proprietăţi, vom specifica acest lucru ori de câte ori va fi nevoie. în fond această lucrare nu este una de matematică ci matematica este folosită doar ca limbaj universal pentru exprimarea relaţiilor dintre diverse mărimi.

 

Să presupunem că există un atribut calitativ X, ce aparţine unui obiect oarecare, care are asociat la un moment dat un atribut cantitativ x, ale cărui valori numerice posibile formează o mulţime ordonată {x}. în matematică, această valoare cantitativă x ce poate să aparţină unei proprietăţi X se numeşte mărimea x, şi deoarece ea poate lua orice valoare din {x} se mai numeşte şi variabila x. Să mai presupunem că există o altă proprietate calitativă Y, cu atributul existenţial y, ale cărui valori fac parte din mulţimea {y}, aşadar avem o altă mărime (sau variabilă) y. Dacă valoarea y se modifică în urma schimbării valorii x şi rămâne invariantă dacă şi x este invariantă, spunem că între cele două mărimi există o relaţie de dependenţă. Această relaţie poate fi univocă (într-un singur sens) sau biunivocă (de interdependenţă). Deocamdată, pe noi ne interesează doar relaţia de dependenţă univocă, caracterul univoc fiind pe mai departe subînţeles când vorbim de dependenţă. Mulţimile de valori numerice {x} şi {y} pe care le-am menţionat mai sus, au ca elemente fundamentale (nedecompozabile) - valorile numerice singulare.

 

 

Comentariul 2.2.2: Asocierea proprietăţii "invariantă" unei variabile pare la prima vedere cam bizară, de aceea este necesară o explicaţie. La un moment dat, când se atribuie valori numerice concrete unei variabile, atât variabila independentă cât şi cea dependentă au atribuită câte o singură valoare. Este adevărat că cele două variabile pot lua orice valoare singulară din domeniul lor de valori, dar prin atribuiri repetate, succesive, pentru fiecare valoare în parte. între două atribuiri, valorile variabilelor rămân invariante. Cititorul va înţelege mai bine acest lucru după parcurgerea în întregime a acestui capitol, deoarece faptul că un atribut cantitativ (valoarea numerică a unei variabile) nu poate avea la un moment dat decât o singură valoare, va rezulta ca o consecinţă a modului specific filosofiei obiectuale de definire a distribuţiilor.

 

 

Cu alte cuvinte, mărimea y nu poate fi modificată în nici un alt fel, decât prin intermediul mărimii x. în sintaxa matematică literală, unul din modurile posibile de a scrie aceste relaţii de dependenţă este:

 

                                                                                                                         (2.2.1)

unde  este numărul de ordine al valorilor numerice din mulţimea ordonată {x}.

 

                                       

                                                     (2.2.2)

 

 

Frontierele unui domeniu pot să facă parte din acesta (să fie frontiere incluse în domeniu), caz în care spunem că intervalul este închis, sau să nu facă parte (să fie doar adiacente domeniului), caz în care avem un interval deschis (cu frontiere asimptotice).

Sublinierile din definiţia 2.2.4 au rostul de a atrage atenţia cititorului că pentru a exista un domeniu de valori trebuie neapărat să existe cele două frontiere ale sale, iar valorile lor să satisfacă relaţia 2.2.2. Nu sunt admise formulări de genul "interval nul" sau "interval vid" deoarece în această lucrare un obiect ce are atributul existenţial (cantitativ) nul înseamnă că nu există.

 

 

Cazul VAE este discutat pe larg în anexa X.3, aici vom spune doar că astfel de valori formează aşa numita "mulţime a numerelor reale" {R} din matematici, şi că fiecare din aceste valori conţine o cantitate infinită de informaţie cantitativă (având o infinitate de cifre), aşadar ele sunt de fapt numere virtuale[1].

Fiecare din mărimile implicate în relaţia 2.2.1 poate lua valori numerice singulare aflate  într-un anumit domeniu (un anumit interval de valori) numit domeniul variabilei independente, respectiv domeniul variabilei dependente (mulţimile {x} şi {y} menţionate mai sus). în cazul cel mai general de dependenţă, fiecărei valori singulare x_k îi corespunde o anumită relaţie f_k şi o anumită valoare y_k, aşa cum indică relaţia 2.2.1.

 

 

Comentariul 2.2.3: Vom vedea după parcurgerea capitolului următor, în care este definită mulţimea set, că şi mulţimea suport a unei distribuţii este o astfel de mulţime (ce nu conţine obiecte identice, adică valori numerice singulare identice). Mulţimile {y} şi {f} pot fi seturi, dar în general lor nu li se impune o astfel de condiţie.

 

Atributul calitativ ale cărui valori cantitative formează mulţimea {y} se mai numeşte în această lucrare şi atribut distribuit, iar cel ale cărui valori formează mulţimea {x} se mai numeşte atribut suport. Poate nu mai este necesar, dar pentru orice eventualitate mai precizăm o dată: cele trei mulţimi {y}, {f} şi {x} au acelaşi număr de elemente (sunt mulţimi echipotente).

 

 

în cazul distribuţiilor virtuale cu suport continuu, suportul îl constituie de obicei un interval din mulţimea numerelor reale {R}, care mulţime, aşa cum precizam mai sus, conţine un număr infinit de valori singulare în orice interval, rezultând de aici că şi numărul relaţiilor dintr-o distribuţie pe un astfel de domeniu ar trebui să fie infinit. Problema se simplifică dacă pe domeniul suport (sau pe subdomenii ale sale) relaţia f este invariantă[3] (independentă de valorile concrete, numerice, pe care le ia x). Respectiva relaţie este în acest caz, clasica funcţie continuă din analiza matematică (unde termenul "continuă" se referă atât la continuitatea suportului, cât mai ales la continuitatea existenţei aceleaşi relaţii de dependenţă pe domeniul suport), valabilă pe domeniul pe care se menţine această invarianţă. Funcţiile continue sunt prin urmare cazuri particulare de distribuţii.

Avantajul esenţial al funcţiilor continue este acela că substituie o infinitate de relaţii individuale (pentru fiecare valoare numerică suport), printr-una singură, valabilă pe domeniul său suport (domeniul de continuitate). Majoritatea distribuţiilor virtuale (matematice) sunt formate din câteva astfel de relaţii invariante (funcţii), definite pe subdomenii continue ale domeniului suport, reuniunea acestor subdomenii alcătuind suportul global al distribuţiei.

Comentariul 2.2.4: De exemplu distribuţia Heaviside (funcţia treaptă unitate) cu referinţa internă x₀ (o VAE din {R}) este definită astfel:

 

                                                                                                 (2.2.3)

 

Observăm că sunt definite două funcţii continue , valabilă pe subdomeniul suport deschis şi , valabilă pe subdomeniul suport semideschis . Reuniunea celor două subdomenii va forma domeniul suport total al distribuţiei, . Distribuţia Heaviside este formată aşadar din două relaţii invariante (funcţii continue), fiecare cu propriul subdomeniu suport (poate fi considerată ca un sistem de două funcţii).

 

în cazul cel mai general de distribuţie primară, când relaţiile de atribuire nu sunt deloc invariante, avem câte o relaţie distinctă pentru fiecare valoare singulară a mărimii suport (este cazul distribuţiilor sub formă de liste, tabele, matrici, imagini etc.).

 

Comentariul 2.2.5: Un caz simplu de astfel de distribuţie este distribuţia Dirac d(x), care în cazul impuls unitate poate fi definită astfel:

 

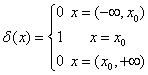                                                                                                 (2.2.4)

 

Putem remarca existenţa a două funcţii continue ca în cazul distribuţiei Heaviside, definite pe două intervale deschise, dar şi existenţa unei relaţii de atribuire distincte pe o valoare singulară x₀, referinţa internă a distribuţiei (despre noţiunea de referinţă internă vom discuta în capitolul următor).

 

Din cele spuse până aici rezultă că o distribuţie primară este decompozabilă până la elementul său fundamental - relaţia individuală de atribuire dintre o valoare singulară a atributului distribuit (dependent) şi o valoare singulară a atributului suport (relaţia 2.2.1) - chiar şi în cazul distribuţiilor primare continue (funcţiile algebrice).

 

Comentariul 2.2.6: Atunci când facem graficul unei funcţii continue, algebrice, pe un calculator, acesta va folosi printr-un proces repetitiv de atâtea ori relaţia de atribuire dintre valoarea atribuită şi valoarea suport, câte valori concrete (singulare) există în domeniul suport. Modul de definire a distribuţiilor în această lucrare trebuia să fie consistent cu POS, enunţat în cap. 1, din acest motiv o distribuţie trebuie tratată ca un sistem decompozabil până la un element fundamental şi compozabil până la limita domeniului maxim posibil al atributului suport. POS este unul din principiile de bază ale acestei lucrări, aşa că la fiecare expunere a noilor obiecte bazate pe distribuţii, în capitolele ce urmează se va insista pe (de)compozabilitatea lor.

 

Aşadar componentele unui element k de distribuţie primară sunt y_k, f_k şi x_k. Dependenţa dintre valoarea singulară distribuită şi cea suport o mai putem scrie sub forma unui produs:

 

                                                                                                                (2.2.5.a)

sau:

                                                                                                     (2.2.5.b)

 

unde r_k (în cazul unui element de distribuţie) este o simplă valoare numerică.

 

 

Cu alte cuvinte, densitatea este un atribut specific doar elementelor unei distribuţii, este aşadar o mărime locală pentru o distribuţie dată. Dacă însă relaţia de atribuire este dependentă de valoarea suport printr-o relaţie  şi această dependenţă este invariantă pe domeniul suport, atunci se poate vorbi de o funcţie densitate a unei distribuţii (în cazul nostru a unei distribuţii primare).

Relaţiile de atribuire pot fi mai simple sau mai complicate[4], gradul lor de complexitate determinând şi complexitatea distribuţiilor. Am văzut mai înainte că o distribuţie este mai simplă dacă relaţia de atribuire este invariantă pe domeniul suport (o funcţie continuă). în acest caz, iarăşi există relaţii (funcţii) mai simple sau mai complicate; cea mai simplă relaţie de acest tip este o constantă numerică (o valoare numerică invariantă), atribuită uniform pe întreg domeniul suport, de unde şi numele unei astfel de distribuţii - distribuţia uniformă[5].

Acest tip de distribuţie având cea mai simplă funcţie de atribuire este o distribuţie fundamentală, ca urmare ea poate fi folosită ca element al unor distribuţii mai complexe. Pe o treaptă imediat superioară distribuţiilor uniforme din p.d.v. al complexităţii relaţiei de atribuire se află distribuţiile liniare (sinonim uniform variabile), numite astfel deoarece într-o reprezentare grafică ele se prezintă ca linii drepte.

Comentariu 2.2.7: De exemplu distribuţia:

 

                                                                                                                (2.2.6)

 

este o astfel de funcţie liniară (ecuaţia unei drepte ce intersectează axa y în y₀), unde mărimea m invariantă pentru o distribuţie dată se numeşte coeficient unghiular al distribuţiei, fiind egală cu tangenta unghiului făcut de dreapta respectivă cu axa X (atributul suport). Se observă că dacă m este nul, distribuţia liniară devine o distribuţie uniformă.

Am discutat până acum despre relaţiile dintre valorile singulare ale celor două atribute implicate într-o distribuţie primară; să vedem ce relaţii există între variaţiile valorilor numerice ale celor două atribute, adică între anumite intervale (ce conţin mulţimi de valori singulare) ale celor două variabile. Pentru aceasta să presupunem că întregul domeniu suport  al unei distribuţii primare {f} îl divizăm în intervale (variaţii) elementare[6] de aceeaşi mărime  (mărime dată de relaţia 2.2.2 şi dictată de condiţia de elementaritate), aşadar domeniul suport este format dintr-un şir ordonat de intervale (variaţii) cu mărime uniformă , concatenate, în care fiecare element al şirului are o poziţie definită (în şir) prin valorile singulare ale frontierelor sale. Astfel, un interval suport ce are frontiera inferioară la ,  iar pe cealaltă la , îl vom nota (provizoriu) cu (atenţie, de această dată m este numărul de ordine al obiectului interval  din şirul ordonat de intervale, număr diferit de k din distribuţia primară).

Dacă se respectă condiţia de elementaritate a intervalelor suport, pe intervalul  orice distribuţie primară {f} poate fi aproximată cu o distribuţie liniară (o funcţie continuă pe ), adică f₁ = f₂ = f_m , rezultând pentru mărimea distribuită o variaţie:

 

                                            (2.2.7)

 

unde  este numărul de ordine al intervalului  în şirul intervalelor  în care este divizat suportul {x}.

Relaţia 2.2.7 este similară cu relaţia 2.2.1, numai că ea defineşte o dependenţă dintre mulţimea  a variaţiilor finite elementare ale mărimii y şi mulţimea  a variaţiilor finite elementare ale mărimii x, unde x şi y, să nu uităm, sunt mărimi ale căror valori singulare sunt legate prin distribuţia primară {f}. Variaţiile  care satisfac condiţia de elementaritate informaţională se mai numesc diferenţe finite de ordinul I ale variabilei y, iar variaţiile , diferenţe finite de ordinul I ale variabilei suport x.

 

Comentariul 2.2.8: Este foarte important ca cititorul să observe că modul de definire al intervalului elementar în filosofia obiectuală nu conţine nicio referire la mărimea acestui interval, singura condiţie de îndeplinit este ca în acest interval să avem o variaţie uniformă a atributului distribuit (sau variaţia reală a acestuia să poată fi considerată uniformă, cea a suportului fiind uniformă prin definiţie). Din acest motiv putem utiliza diferenţele finite (a căror mărime nu contează în această situaţie).  Un exemplu în anexa X.2.

 

 

în cazul distribuţiei derivate de ordinul I, mulţimea  a variaţiilor finite de ordinul I ale atributului y constituie noul atribut distribuit, iar mulţimea ordonată a variaţiilor finite  constituie suportul acestei distribuţii. Este evident şi de această dată că mulţimile ,   şi  au acelaşi număr de elemente (dar diferit de cel al mulţimilor distribuţiei primare din care derivă, în raportul ,  şi  fiind numărul de elemente ale mulţimii {x}, respectiv ).

 

Comentariul 2.2.9: Este iarăşi important să observăm că elementul fundamental (nedecompozabil) al distribuţiei derivate de ordinul I este o variaţie uniformă (o mulţime de valori singulare, un interval)  atribuit printr-o relaţie  unei variaţii uniforme , în timp ce distribuţia primară (din care provine distribuţia derivată) are ca element fundamental, aşa cum arătam mai sus, o valoare singulară y_k atribuită printr-o relaţie f_k unei valori singulare x_k. Cititorul va înţelege mai bine diferenţa dintre relaţiile 2.2.1 şi 2.2.7 după parcurgerea capitolului următor în care vom defini ce înseamnă obiect, ce este o referinţă internă şi mai ales după parcurgerea cap 4, în care vom vedea ce înseamnă o variaţie a valorii unui atribut, adică un proces. Vom vedea astfel că deşi în ambele relaţii este prezentă aceeaşi valoare singulară x_k , în relaţia 2.2.1 x_k este un obiect de tip valoare singulară, iar în relaţiile 2.2.7 x_k este tot un obiect de tip valoare singulară dar şi referinţă internă a unui obiect de tip interval.

 

La fel ca şi în cazul distribuţiilor primare, dacă relaţia de dependenţă  se menţine aceeaşi pe întreg domeniul variabilei independente (în cazul nostru, al mulţimii , indiferent de valoarea concretă a lui m), respectiva relaţie este o funcţie continuă pe acel interval, funcţie numită derivata de ordinul I a funcţiei primare f. Tot ca în cazul distribuţiilor primare, şi la distribuţiile derivate de ordinul I, elementul distribuţiei îl putem scrie sub formă de produs:

 

                                                                                                         (2.2.8.a)

 

sau:

                                                                                           (2.2.8.b)

 

unde  este tot densitatea elementului de distribuţie, de această dată a distribuţiei derivate de ordinul I.

Comentariul 2.2.10: Dacă în relaţiile 2.2.8 înlocuim ecuaţia unei distribuţii liniare dată de relaţia 2.2.6 obţinem:

 

                                                                                (2.2.9)

de unde rezultă :

                                                                                                          (2.2.10)

 

adică densitatea unui element de distribuţie derivată (care este densitatea unei distribuţii primare liniare) este tocmai coeficientul unghiular, tangenta unghiului făcut de distribuţia liniară primară faţă de axa variabilei independente (suportul distribuţiei). Densitatea distribuţiilor primare nu are nicio utilitate practică (cel puţin deocamdată), ea fiind introdusă doar pentru a sublinia generalitatea modelului obiectului abstract densitate, valabil pentru orice tip de distribuţie, aşadar şi pentru cele primare. Densităţile distribuţiilor derivate, aşa cum vom vedea în capitolele următoare, sunt obiecte abstracte de mare importanţă în acestă lucrare pentru caracterizarea proceselor, fiind substitutele derivatelor locale din calculul diferenţial, valabile şi pentru distribuţiile cu suport discontinuu (vezi anexa X.2.1).

 

Este destul de clar pentru cititor că distribuţiile derivate ale unei distribuţii primare f  pot fi şi de ordine mai mari, cu menţiunea că singura distribuţie primară rămâne f, toate celelalte fiind distribuţii derivate , elementele tuturor acestor distribuţii având acelaşi suport (intervalul elementar ), diferind doar mărimea distribuită (o diferenţă finită de ordinul n) şi numărul de elemente al distribuţiei. Pentru toate aceste distribuţii, criteriul de elementaritate este acelaşi, la fel şi definiţiile pentru elementul de distribuţie şi pentru densitatea acestuia.

Nu putem încheia acest paragraf fără a face nişte observaţii privind diferenţele dintre obiectele matematice introduse aici şi obiectele din matematicile clasice (diferenţe care există şi în alte domenii matematice şi care sunt tratate pe larg în anexa X.3). în primul rând iese în evidenţă preocuparea filososfiei obiectuale pentru structura clară a fiecărui obiect (abstract) folosit, mai ales pentru elementele nedecompozabile ale acestei structuri - elementele fundamentale. Odată definite aceste elemente şi relaţiile dintre ele, rezultă o structură coerentă a întregului ansamblu (obiectul compus din aceste elemente), chiar dacă acest obiect arată (şi este denumit altfel) decât în matematica oficială. Dacă între distribuţiile primare şi distribuţiile din matematici nu există diferenţe prea mari (înafara conceptului neobişnuit de densitate a unui element sau a unei funcţii), nu aceeaşi situaţie este cu distribuţiile derivate, unde diferenţele sunt majore. Modul de definire al distribuţiilor derivate (şi implicit al funcţiilor derivate) este mult diferit de cel folosit în calculul diferenţial. Un obiect similar cu derivata locală de ordinul n clasică a unei funcţii f este în filosofia obiectuală densitatea unei distribuţii derivate de ordinul n a respectivei funcţii.