X.15.1 Vectorul densitate de flux (VDF)

Densitatea este o mărime caracteristică numai distribuţiilor uniforme, şi reprezintă o mărime abstractă (rezultatul unui proces abstract, de calcul) dată de raportul dintre mărimea distribuită şi mărimea domeniului suport al distribuţiei. în termeni mai uşor de înţeles, densitatea reprezintă gradul de "înghesuire" a mărimii distribuite pe intervalul suport, sau (pentru atributele cumulative) cantitatea de atribut distribuit pe suportul abstract de mărime unitate. Fiind o mărime abstractă, densitatea nu poate exista în lipsa unui SSI care să-i conţină valoarea şi a unui SPI care să o fi calculat, dar utilizarea sa este foarte largă fiind printre altele singurul atribut ce permite evaluarea intensităţii proceselor.

 Intensitatea unui proces distribuit de mişcare se evaluează cu ajutorul unei suprafeţe virtuale (teoretice, imaginare, de calcul) cu poziţie spaţială fixă faţă de o referinţă externă (aceeaşi referinţă faţă de care se evaluează viteza de mişcare distribuită).

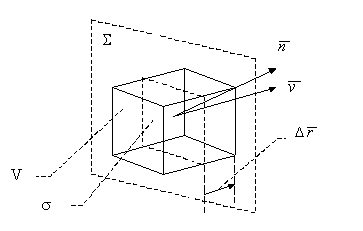
Fig. X.15.1.1

Fie volumul V din fig. X.15.1.1 ce conţine mărimea M, uniform distribuită cu densitatea:

                                                                                                                 (X.15.1.1)

şi o suprafaţă plană teoretică de referinţă , cu poziţie fixă faţă de o referinţă externă.

Referinţa internă T (cu poziţie internă centrală) a volumului V are faţă de aceeaşi referinţă externă vectorul de poziţie (nefigurat în fig. X.15.1.1 pentru a nu complica desenul). Să presupunem că la un moment t₀, volumul V, cu tot cu mărimea M distribuită uniform în el, începe să se mişte cu viteza:

                                                                                                                    (X.15.1.2)

considerată uniformă (constantă) în intervalul Dt. Intersecţia dintre volumul V aflat în mişcare şi suprafaţa de referinţă  este , o suprafaţă cu normala (aceeaşi cu normala la ) prin care are loc transferul (deplasarea) mărimii M. în intervalul  va trece prin suprafaţa  o cantitate:

                                                                                       (X.15.1.3)

Dacă împărţim relaţia X.15.1.3 cu  obţinem:

                                                         (X.15.1.4)

relaţie identică cu relaţia 5.2.1.4 ce defineşte în filosofia obiectuală intensitatea fluxului vectorului  prin suprafaţa . Acest vector  are o mare importanţă în această lucrare, fiind denumit vector densitate de flux (VDF) al mărimii M. Observăm că VDF este întotdeauna colinear cu viteza de transfer, el fiind vectorul purtător al mărimii abstracte , densitatea volumică a mărimii de transportat. în acest fel, fluxul mărimii M poate fi reprezentat ca o distribuţie vectorială a VDF (un câmp vectorial). Dacă distribuţia de volum a mărimii M nu este uniformă, vom diviza volumul V în elemente de volum dV cu dimensiuni astfel alese încât în interiorul lor distribuţia mărimii M să fie uniformă. Intersecţia unui astfel de element cu suprafaţa  va fi  iar intensitatea fluxului prin  va fi:

                                                               (X.15.1.5)

adică intensitatea unui flux elementar. Dacă în relaţiile X.15.1.4 şi X.15.1.5 facem raportul dintre intensitatea fluxului şi mărimea suprafeţei  sau  obţinem densitatea superficială a intensităţii fluxului:

                                                                                       (X.15.1.6)

Apare astfel clară semnificaţia VDF, modulul componentei normale a VDF prin suprafaţa de referinţă este tocmai densitatea superficială a intensităţii fluxului mărimii transportate prin acea suprafaţă.

Comentariul X.15.1.1: Observăm că VDF are în compunere un atribut cumulativ – densitatea volumică a mărimii transportate – fapt ce face ca şi VDF să devină un atribut cumulativ. Astfel mulţimea vectorilor VDF uniform distribuiţi fie pe suprafaţă, fie pe volum, având o direcţie comună, poate fi înlocuită (reprezentată) de un singur vector – rezultanta – ce va avea direcţia comună iar modulul egal cu suma (integrala de volum sau suprafaţă) a VDF.