X.15.2 Componentele locale ale VDF

Pentru o suprafaţă de referinţă oarecare (nu neapărat plană), în fiecare punct al acestei suprafeţe există o normală  şi un plan perpendicular pe normală, planul tangent P_t (vezi fig. X.15.2.1) ce trece prin punctul de aplicaţie al normalei (referinţa T locală).

 

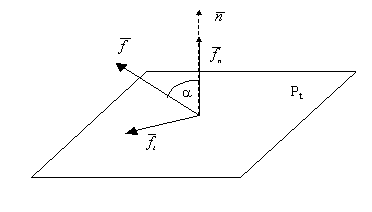
Fig. X.15. 2.1

Având direcţia unghiulară  faţă de normală ca direcţie de referinţă, VDF al unui flux oarecare ce traversează suprafaţa, are cele două componente vectoriale: componenta comună cu normala  şi componenta specifică faţă de normală , ambele componente satisfăcând relaţia:

                                                                                                            (X.15.2.1)

Deoarece cele două componente sunt perpendiculare între ele (independente direcţional), adică  este inclusă în planul tangent, toate elementele relaţiei X.15.2.1 sunt coplanare. Cele două componente locale (punctuale) ale VDF sunt date de funcţiile C() şi D() introduse în cap. 4, funcţii ce ne dau componenta comună şi specifică ale unui vector faţă de o direcţie de referinţă.

 

                                                                            (X.15.2.2)

 

                                                                             (X.15.2.3)

 

Comentariul X.15.2.1: Aici apar doi operatori c şi s introduşi pentru a evita confuzia cu operatorii deja existenţi în calculul vectorial, produsul scalar şi produsul vectorial, ale căror formule sunt asemănătoare (c cu produsul scalar iar s cu produsul vectorial), dar rezultatele sunt total diferite.

 

Până aici am prezentat cazul simplu când printr-un punct al suprafeţei de referinţă trece un singur VDF. Să presupunem acum că prin aceeaşi suprafaţă trec N fluxuri, existente simultan, de acelaşi tip, dar din surse diferite aflate la poziţii spaţiale diferite, având prin urmare direcţii şi intensităţi diferite. Traversând suprafaţa de referinţă prin acelaşi punct, referinţa T locală, toţi VDF ai celor N fluxuri ce trec prin acelaşi punct vor forma un "buchet" de vectori concurenţi, aşadar pentru ei poate fi evaluată o componentă comună şi N componente specifice toate incluse în planul normal pe componenta comună.

 

Comentariul X.15.2.2: Din afirmaţia că VDF şi cele două componente locale ale sale sunt vectori coplanari rezultă că numai componenta comună colineară cu normala este unică, toate cele N componentele specifice fiind incluse în planul tangent, dar cu direcţii diferite  ().

 

Aici apar două cazuri, în funcţie de tipul de direcţie de referinţă pe care o alegem pentru mulţimea celor N vectori:

1.    Referinţă artificială, cazul discutat anterior, în care direcţia de referinţă (direcţia componentei comune) este direcţia normalei. Faţă de această direcţie se evaluează:

                                  (X.15.2.4)

 

                                                                 (X.15.2.5)

 

2.    Referinţă naturală, caz în care de obicei direcţia de referinţă nu coincide cu direcţia normalei ci are faţă de normală direcţia unghiulară  ( este unghiul dintre componenta comună naturală şi normala din acel punct, evaluat în planul ce include cei doi vectori). Direcţia referinţei naturale rezultă din proprietatea fundamentală a sa, aceea că faţă de o referinţă naturală, componenta comună a mulţimii componentelor specifice este nulă (inexistentă), adică:

                                                                                                         (X.15.2.6)

 

unde componentele specifice naturale sunt incluse într-un plan perpendicular pe direcţia de referinţă naturală (nu în planul tangent anterior), dar care plan trece tot prin punctul comun de aplicaţie al tuturor vectorilor (referinţa T locală).

în cazul referinţei artificiale, relaţia X.15.2.6 nu este obligatorie, dimpotrivă, putem avea:

                                                                                                              (X.15.2.7)

 

adică suma componentelor specifice (tangenţiale) ale mulţimii celor N VDF concurenţi are o rezultantă diferită de zero, o componentă comună cu direcţia .

 

Comentariul X.15.2.3: Dacă cititorul a parcurs deja cap. 7 în care sunt descrise procesele de (des)compunere a fluxurilor pe suprafeţele reale de separaţie (SRS) ale sistemelor materiale, cazul existenţei unei rezultante nenule pentru componentele specifice (tangenţiale) ale mai multor fluxuri se traduce prin existenţa unei componente coerente tangenţiale a fluxului rezultant, componentă ce poate avea o circulaţie nenulă pe SRS. Iar unde există o circulaţie, există şi o distribuţie rotorică în volumul cuprins de SRS (teorema lui Stokes).