X.24.8.1 Distribuţia Plank

După tratatele de specialitate[1] puterea emisă pe unitatea de arie, de către un corp negru[2], aflat la temperatura T, într-un interval elementar de lungimi de undă este:

 

                                                                                         (X.24.8.1.1)

unde este dată de relaţia :

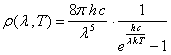                                                                                   (X.24.8.1.2)

 

 

h fiind constanta lui Plank, k fiind constanta lui Boltzmann, iar c viteza luminii. Relaţia X.24.8.1.2 este binecunoscuta distribuţie Plank a fotonilor termici emişi de un corp negru aflat la temperatura T, distribuţie având ca suport intervalul infinit al lungimilor de undă fotonice.

Relaţiile de mai sus, transformate pentru domeniul frecvenţă devin:

 

                                                                                          (X.24.8.1.3)

 

iar densitatea frecvenţială (spectrală) a puterii emise:

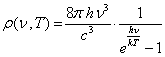                                                                                    (X.24.8.1.4)

 

 

Reamintim cititorului că din p.d.v. al tipului de obiect abstract, distribuţia Plank având ca suport atributul frecvenţial (sau lungimea de undă) constituie un spectru. Reprezentarea grafică a acestui spectru, în care atât atributul frecvenţial suport cât şi atributul distribuit sunt substituite (reprezentate) de atributul poziţie spaţială, devine însă o formă 2D a spectrului.

Recunoaştem în relaţia X.24.8.1.4 termenul  ca fiind energia conţinută într-un foton cu frecvenţa , iar termenul kT (din ecuaţia gazelor perfecte) ca fiind tot o energie, energia termică menţionată în ecuaţia X.24.7.1. Deocamdată ştim că această energie kT are o valoare invariantă dacă temperatura corpului negru este invariantă, şi corespunzător acestei valori, şi forma distribuţiei Plank este invariantă. Cu aceste precizări observăm că exponentul lui e din relaţia de mai sus este o mărime adimensională (un număr, raportul a două energii) pe care o notăm x şi care are domeniul de variaţie tot . Cu această schimbare de variabilă, relaţia X.24.8.1.4 devine:

                                                               (X.24.8.1.5)

unde  este o relaţie unică pentru toate distribuţiile Plank. Relaţia X.24.8.1.5 este numită în această lucrare distribuţie Plank normalizată. Funcţia f(x) integrată pe domeniul său suport  are o valoare finită, egală cu . Rezultă că puterea totală radiată pe unitatea de arie de un corp negru aflat la temperatura T este:

                                                                                               (X.24.8.1.6)

 

putere care înseamnă intensitate a fluxului de energie termică radiată, energie conţinută în fotonii termici emişi de respectivul corp. Relaţia X.24.8.1.6 scrisă sub forma:

                                                                                                       (X.24.8.1.7)

unde e este un coeficient numit emisivitate[3]  a suprafeţei corpului (egală cu unu pentru corpul negru), iar  o constantă numită

 

constanta lui Stefan, devine relaţia Stefan-Boltzmann. în această relaţie, cititorul poate observa că acest coeficient de emisivitate e, în termeni specifici filosofiei obiectuale, nu este altceva decât permeabilitatea SRS a corpului radiant la influxul interior de fotoni termici.

Dar să revenim la funcţia f(x) a cărei reprezentare este dată în fig. X.24.8.1.1, unde este dată şi reprezentarea derivatei f‘(x), pentru a se putea vedea mai uşor poziţia maximului acestei funcţii.

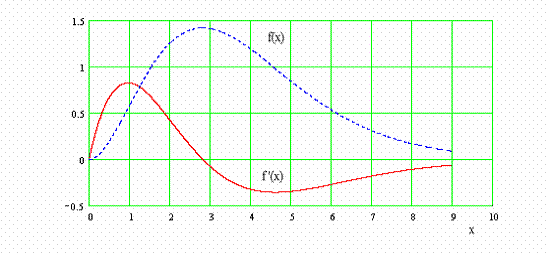
Fig. X.24.8.1.1

După cum se poate observa din figură, trecerea prin zero a derivatei (ce corespunde maximului f(x)) are loc pentru o valoare x_R care este soluţia ecuaţiei rezultată din anularea derivatei f’(x) :

                                            (X.24.8.1.8)

 

Prin metode numerice, rezultă pentru soluţia nebanală (cea banală fiind x=0) o valoare . Aşadar distribuţia Plank normalizată are un maxim ce corespunde acestei valori unice pentru oricare distribuţie de acest fel. După cum am văzut în capitolele despre distribuţii şi obiecte, şi acestă distribuţie este un obiect abstract care trebuie să se poată deosebi de alte obiecte abstracte din aceeaşi clasă, care are o referinţă internă, referinţă ce reprezintă obiectul în relaţiile sale externe. Cum poziţia maximului tuturor distribuţiilor Plank normalizate este mereu aceeaşi, corespunzătoare valorii:

 ,                                                  (X.24.8.1.8)

 

rezultă că singurul tip de atribut prin care două distribuţii Plank normalizate pot diferi este valoarea acestui maxim (amplitudinea densităţii) ce corespunde valorii suport x_R (în termeni specifici acestei lucrări, valoarea atributului distribuit pe valoarea singulară x_R ). Dar noi am văzut că o valoare invariantă pentru o clasă de obiecte, faţă de care se evaluează atributele obiectelor, constituie o referinţă. Aşadar x_R este o referinţă internă, şi deoarece valoarea sa nu este impusă de un SPI ci se autostabileşte în urma interacţiunilor dintre elementele mediului atomic şi cele ale mediului fotonilor termici interstiţiali, rezultă că x_R este o referinţă naturală.