X.3.2.2.1 Familii de obiecte abstracte şi asimptotele lor

în geometria analitică este cunoscut termenul de "familie de curbe", termen ce simbolizează o mulţime de funcţii continue pe un interval comun, care diferă între ele ca relaţie de dependenţă simbolică doar prin valoarea unui parametru. De exemplu familia dreptelor ce trec prin origine au o relaţie generală y = mx, unde m (coeficientul unghiular) este parametrul; ca un caz particular, pentru dreptele ce au o direcţie unghiulară cuprinsă în intervalul  faţă de axa X, m poate lua orice valoare între -1 şi +1. în acest caz, familia de curbe nu are asimptote, parametrul m putând lua şi valorile extreme (frontierele intervalului). Cu totul alta este situaţia în cazul când există o anumită valoare numerică de care parametrul se poate apropia oricât de mult, dar care valoare dacă ar fi atinsă, ar schimba calitativ modelul obiectului (tipul de distribuţie), acest nou obiect nemaifăcând parte din familie. Pentru a ilustra un astfel de caz vom considera în fig. X.3.2.2.1.1 familia de hiperbole din primul cadran xy=C, unde C este o constantă numerică pozitivă (parametrul), cu o valoare precizată pentru o anumită hiperbolă din familie.(un anumit membru al familiei).

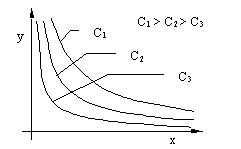
Fig. X.3.2.2.1.1

Este evident că axele de coordonate sunt asimptotele familiei de hiperbole pentru parametrul C tinzând spre zero, dar dacă am accepta că hiperbolele şi asimptotele lor fac parte din aceeaşi familie (deci au acelaşi model, aceeaşi relaţie simbolică de distribuţie), am ajunge la concluzia absurdă că şi axele de coordonate sunt o hiperbolă (stilizată, nu ? (#)). Exact aceeaşi situaţie o avem şi în cazul relaţilor X.3.2.2.3 şi X.3.2.2.4, care definesc o familie de raporturi ale unor diferenţe finite simetrice (stânga/dreapta) ale unei funcţii faţă de o valoare de referinţă, familie al cărei parametru este Dx. Această familie are ca asimptotă direcţională direcţia tangentei în P, obiect spre care tind cele două variaţii, dar care nu le poate substitui, deoarece sunt obiecte diferite calitativ.

Să interpretăm datele de mai sus folosind terminologia specifică acestei lucrări introdusă în capitolele 2...9. Astfel, în cazul "familiilor" este clar că este vorba de clase de obiecte abstracte, o clasă fiind un obiect abstract ce are ca model componenta comună a modelelor unei mulţimi de obiecte (membrii, instanţele clasei). în cazul dreptelor ce trec prin origine sau a hiperbolelor de care vorbeam mai sus, componenta comună a tuturor membrilor clasei este relaţia simbolică generală (y=mx în cazul dreptelor şi xy=C în cazul hiperbolelor), fiecare instanţă a claselor respective deosebindu-se doar prin valoarea numerică a parametrului, valoare ce în termeni filosofiei obiectuale reprezintă componenta diferenţială (specifică) a unui membru al clasei de curbe (faţă de ceilalţi membri). Dacă în cazul clasei dreptelor ce trec prin origine relaţia definitorie a clasei nu se schimbă oricare ar fi valoarea parametrului, în cazul hiperbolelor apare o situaţie interesantă când parametrul tinde la zero, şi anume, cât timp acest parametru (C) este diferit de zero, înseamnă că relaţia de dependenţă hiperbolică dintre y şi x încă există; în momentul anulării parametrului, dispare şi relaţia de dependenţă, cele două mărimi devenind independente (axele de coordonate), aşa cum am stabilit în cap.2 referitor la noţiunea de independenţă a variabilelor. Este foarte clar că în acest caz obiectele limită ale clasei (asimptotele) şi obiectele normale ale clasei sunt diferite calitativ ca model de clasă, în timp ce membrii clasei, între ei, sunt diferiţi doar prin valorile componentei specifice.