X.3.2.2 Derivata clasică a unei funcţii continue

Una din cele mai concise expuneri ale conceptului de derivată conform calculului diferenţial clasic o găsim în Manualul Inginerului[1].

Definiţia derivatei. Fie y=f(x) o funcţie continuă într-un interval (a, b) şi un punct x₀ în interiorul lui. Prin definiţie se numeşte derivata funcţiei în x₀ limita către care tinde raportul dintre creşterea funcţiei şi creşterea variabilei când aceasta din urmă tinde către zero. Vom nota cu:

                                           (X.3.2.2.1)

Dacă această limită există, vom spune că funcţia f(x) este derivabilă în x₀. Dacă facem graficul funcţiei f(x), derivata într-un punct al ei reprezintă coeficientul unghiular al tangentei la curbă. Se poate întâmpla ca limita acestui raport să aibă într-un punct două valori, după cum  tinde spre zero prin valori pozitive sau negative; vom spune că avem o derivată la stânga sau la dreapta.

Diferenţiale. Fie y=f(x) o funcţie derivabilă într-un interval (a, b) şi fie x o variabilă cuprinsă în acest interval. Creşterea variabilei dx o vom numi diferenţiala variabilei. Prin definiţie vom numi diferenţiala funcţiei valoarea:

                                                                                                         (X.3.2.2.2)

Pentru a comenta definiţiile de mai sus avem în fig. X.3.2.2.1 următoarele elemente:

-     curba f(x) pe care există un punct curent ;

-     tot pe curbă, mai avem alte două puncteşi, unde  iar;

-     tangenta la curba f(x) în punctul P, pe care avem punctele  şi ;

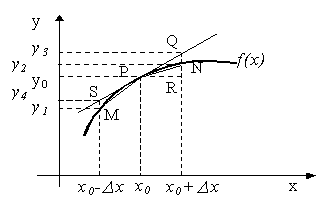
Fig.  X.3.2.2.1

Observăm că punctele M, P şi N aparţin curbei f(x), în timp ce punctele Q şi S nu, dar în calculul diferenţialelor la stânga sau dreapta punctului P intervin tocmai valorile din Q şi S, cu toate că ele nu aparţin funcţiei (de exemplu diferenţiala la dreapta lui P este reprezentată conform definiţiei de segmentul RQ, în timp ce variaţia reală este RN). în cazul în care valorile funcţiei din M, P şi N sunt obţinute prin eşantionare, nici nu se poate vorbi de valorile din Q şi S, aceste valori fiind pur abstracte (generate prin calcul). Pe graficul din fig, X.3.2.2.1, linia ce uneşte două puncte de pe curbă, de exemplu PM este o secantă a curbei f(x). Această secantă are faţă de axa de referinţă (axa valorilor mărimii independente) X, o direcţie unghiulară  (evaluare la stânga referinţei , dată de relaţia:

                                                                  (X.3.2.2.3)

iar secanta PN are faţă de aceeaşi axă de referinţă direcţia unghiulară  (evaluare la dreapta referinţei ), dată de relaţia :

                                                                 (X.3.2.2.4)

ambele relaţii fiind valabile pentru orice interval finit şi nenul , dar după cum ne arată relaţia X.3.2.2.1, în definirea derivatei clasice, la un moment dat acest interval devine nul (în punctul P), acolo unde calculul diferenţial clasic defineşte derivata în punctul P.