X.3.5 Vectori

Aşa cum am văzut în cap. 4, reprezentarea matematică a proceselor elementare specifice (PES) se face prin vectori. Legat de noţiunile de obiect şi proces, noţiuni fundamentale în prezenta lucrare, şi definiţia noţiunii de vector este puţin diferită faţă de cea din matematica obişnuită, chiar de cea folosită în învăţământul superior. în această lucrare vectorii sunt definiţi ca variaţii cantitative direcţionale uniforme ale unui singur atribut calitativ, între două stări: starea iniţială (ce corespunde punctului de aplicaţie) şi starea finală (ce corespunde într-o reprezentare grafică vârfului vectorului). în acelaşi timp, vectorii sunt obiecte procesuale, care reprezintă totalitatea atributelor invariante (pe domeniul lor suport) ale unor PES date (punctul de aplicare, direcţia, modulul etc.).

Un caz special în care definiţia vectorului din această lucrare este diferită de lucrările actuale este cea a vectorilor purtători, componente ale modelului matematic pentru fluxuri. în lucrările existente, un vector purtător (sau alunecător) este acel vector ce are punctul de aplicaţie mobil. în filosofia obiectuală, acestei descrieri i se mai adaugă atributul de transportat, deoarece un vector purtător trebuie să "poarte" (să aibă ataşată) o mărime ce se va mişca odată cu vectorul, aşa cum vectorului densitate de flux (VDF) îi este ataşată densitatea scalară r a mărimii de transportat.

Deoarece în cazul PES cu suport spaţial vectorii sunt singurele reprezentări pentru atributul direcţie, există o clasă de vectori specializaţi pentru acest lucru - versorii - al căror modul este mereu unitar şi care sunt folosiţi ca referinţe de direcţie (sunt componente ale sistemelor de referinţă R) fie pentru SR externe, fie pentru SR interne, fie pentru SR locale (cum sunt normala, tangenta şi binormala într-un punct al unei curbe în spaţiu).

Datorită modului specific de interpretare a vectorilor în acestă lucrare, unele "artificii" de calcul utilizate în reprezentările geometrice ale vectorilor din calculul vectorial clasic trebuie privite cu discernământ. De exemplu, în fig. X.3.5.1 este reprezentată o operaţie clasică de însumare a doi vectori V₁ şi V₂, ce au un punct comun de aplicare S_1,2.

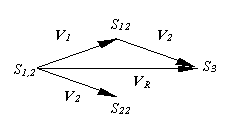
Fig. X.3.5.1

  în calculul vectorial clasic (în care vectorii sunt consideraţi liberi), suma celor doi vectori este diagonala paralelogramului ce are ca laturi vectorii respectivi; aici nu este nicio diferenţă în rezultat dacă cei doi vectori sunt cu originea în acelaşi punct (S_1,2), sau vectorul V₂ este deplasat paralel cu originea în S₁₂, vârful vectorului V₁. Privite din p.d.v. procesual, dacă cei doi vectori sunt PES distribuite pe suport temporal (cazul proceselor reale), faptul că vectorii V₁ şi V₂ au o stare iniţială comună (S_1,2) înseamnă că cele două PES reprezentate sunt simultane, iar dacă V₂ are starea iniţială egală cu starea finală a lui V₁ (S₁₂) atunci cele două PES sunt succesive. în cele două situaţii, vectorul rezultant V_R are un suport temporal diferit (amplitudinea, mărimea, vectorului este aceeaşi în ambele situaţii dar densitatea temporală a PES rezultant este alta).