4.4 Vectori

Pentru PES (indiferent de ordinul lor) există o simbolistică specială, deoarece acest tip de proces este baza (elementul) tuturor celorlalte procese, cu alte cuvinte, orice proces oricât de complex poate fi descompus în astfel de procese elementare. în sintaxa vizuală, atât literală cât mai ales grafică, un astfel de simbol pentru reprezentarea unui PES este vectorul.

Acest simbol este un substitut grafic pentru o variaţie uniformă de atribut, variaţie între două stări: iniţială şi finală (ce corespund celor două frontiere ale intervalului suport). Cele două stări sunt reprezentate prin două puncte ale căror poziţii reprezintă atributele celor două obiecte stare, între acestea existând un segment orientat de dreaptă ce reprezintă variaţia uniformă de stare. Segment orientat înseamnă că s-a impus un anumit sens (simbolizat de sensul săgeţii), sens ce indică o variaţie pozitivă dintre starea iniţială şi cea finală. Mărimea (lungimea) segmentului de dreaptă orientat este proporţională cu mărimea variaţiei dintre cele două stări (amplitudinea variaţiei)[1].

în funcţie de informaţia conţinută în obiectul vector, vom avea mai multe tipuri de astfel de obiecte, ale căror denumiri există deja în literatura ştiinţifică, dar modul lor de tratare este puţin diferit de cel folosit aici:

1)    Vectori liberi, pentru care este cunoscută doar mărimea (modulul), sensul şi direcţia variaţiei, stările iniţială şi finală fiind nedeterminate;

2)    Vectori legaţi, pentru care este cunoscută starea iniţială invariantă (punctul de aplicaţie al vectorului), mărimea şi direcţia variaţiei de stare;

3)    Vectori purtători (în unele publicaţii se mai numesc alunecători), cu aceleaşi atribute ca vectorii legaţi, deosebirea fiind starea iniţială care este variabilă.

Majoritatea vectorilor folosiţi în calculul vectorial şi în teoria câmpurilor vectoriale din matematică sunt vectori liberi. Discipline cum ar fi rezistenţa materialelor sau statica fluidelor operează cu distribuţii vectoriale cu vectori legaţi, dar mai există şi în matematică şi fizică o clasă împortantă de astfel de vectori - vectorii de poziţie (legaţi de originea SR). Vectorii purtători vor fi clasa de vectori folosită în prezenta lucrare ca model matematic pentru fluxuri.

Observăm că în descrierea obiectelor de tip vector, deci şi a PES substituit, apare un nou atribut - direcţia. Acest atribut este foarte important pentru reprezentarea PES, aşa că îl vom analiza mai în detaliu puţin mai încolo.

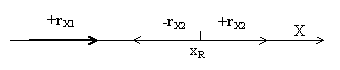
Fig. 4.4.1

în figurile 4.4.1 şi 4.4.2 avem câte o reprezentare în sintaxă vizual-grafică a unor PES (vectori), în două cazuri speciale:

1)      Cazul când atributul variabil are o singură componentă calitativă, în cazul nostru X din fig. 4.4.1, atribut numit şi monodimensional. Acest atribut calitativ are ca domeniu de valori (domeniul atributului existenţial) un segment din mulţimea (virtuală sau realizabilă, vezi anexa X.3) a numerelor reale {R}. O variaţie uniformă a valorii acestui atribut înseamnă o parcurgere uniformă, succesivă, a tuturor valorilor din domeniul lui de valori, de la o valoare iniţială, până la o valoare finală. Restricţia ca toate aceste valori parcurse să fie incluse într-un singur domeniu face ca o astfel de parcurgere să nu poată avea decât două atribute distinctive: sensul pozitiv (considerat prin convenţie ca cel crescător, adică valoarea stării finale este mai mare decât cea a stării iniţiale) şi sensul negativ (situaţia inversă). Acest atribut - sensul - caracteristic proceselor specifice cu atribut monodimensional (1D), poate avea aşadar doar două valori (+ sau -). Observăm că sensul unei variaţii, reprezentat de semnul acesteia, poate fi independent de valorile concrete ale celor două stări (iniţială şi finală), important este doar ca diferenţa dintre acestea să aibă semnul cerut. Acest caz este tipic pentru vectorii liberi, în exemplul din fig. 4.4.1 r_X1. Cu totul alta este situaţia dacă starea iniţială este precizată, în cazul nostru valoarea x_R . în acest caz putem vorbi de un nou obiect abstract, direcţia, pentru cazul nostru monodimensional tot cu doar două valori posibile, corespunzător celor două sensuri posibile ale variaţiei faţă de referinţa x_R  (în fig. 4.4.1 vectorii -r_X2 şi +r_X2 ). Vom vedea în continuare că există un mod de a defini direcţia mai precis în cazul vectorilor cu mai multe dimensiuni.

2)      Cazul în care atributul variabil are două componente calitative independente (vezi definiţia 2.1.2), în cazul nostru X şi Y din fig. 4.4.2, atribut numit şi bidimensional. Vedem în acest caz că un PES oarecare al atributului r(X,Y) este compus din două PES independente (simultane şi monodimensionale) r_X şi r_Y. Aceste componente fiind evaluate faţă de o referinţă comună (originea axelor O), au fiecare direcţia axei în care sunt incluse  (după cum am văzut în cazul 1) stabilită faţă de această referinţă. Mai putem spune că o variaţie (în cazul din fig. 4.4.2 absolută) r a unui obiect compus bidimensional este rezultatul a două variaţii independente (tot absolute) care contribuie fiecare într-o anumită proporţie la variaţia totală. Cele două componente din fig. 4.4.2 reprezintă tocmai aceste contribuţii (numite şi proiecţii).

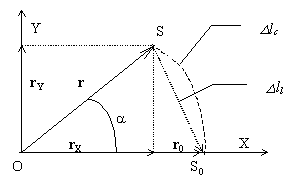
Fig. 4.4.2

Pentru cazul când atributul compus este poziţia spaţială, ştim din geometria analitică de existenţa unor relaţii invariante între modulul vectorului r (variaţia totală de atribut) şi modulele componentelor (proiecţiilor) de pe cele două axe: , . Dar prin prisma celor discutate în cap. 2,  mărimile 

                                                                                                                      (4.4.1.a)

                                                                                                                     (4.4.1.b)

 

sunt în acelaşi timp nişte densităţi ale unor variaţii uniforme (absolute) ale componentelor, pe suportul comun - variaţia totală (densităţile distribuţiilor variaţiilor specifice pe variaţia totală).

 

 

Conform acestei definiţii, direcţiile numerice (versorii) axelor de coordonate sunt X={1,0} şi Y={0,1}. Definiţia 4.4.1 este valabilă şi pentru cazul 3D, adăugându-se evident componenta  faţă de axa cu direcţia Z. Vedem că în cazul unui atribut monodimensional, variaţia totală este identică cu variaţia componentului, aşadar densitatea 4.4.1 este egală cu unu iar contribuţia la variaţie a unei alte mărimi este nulă. Acesta este cazul tipic al axelor de coordonate. Atributul existenţial (modulul) al versorului  este egal cu unu, din acest motiv nu a mai fost menţionat în relaţia 4.4.2. între componentele  şi  există relaţia cunoscută:

                                                                                                                    (4.4.3)

în practică, direcţia unui vector este evaluată mai frecvent prin întermediul unei soluţii a ecuaţiei 4.4.3 şi anume  menţionat mai sus, dat de relaţiile :

                                                                                        (4.4.4)

şi care este un alt tip de atribut existenţial al direcţiei unui vector faţă de referinţa X. Mărimea  din relaţia 4.4.4 reprezintă direcţia unghiulară a vectorului faţă de axa de referinţă.

 

Comentariul 4.4.1: Componentele direcţiilor numerice definite în relaţiile 4.4.1 ca raporturi dintre două variaţii liniare (două procese de tip P₁) sunt în mod clar adimensionale (de aceea le-am şi numit numerice). Direcţiile unghiulare sunt definite în matematici ca raportul dintre lungimea unui arc de cerc (din fig. 4.4.2) şi raza sa, fapt care i-a condus pe matematicieni la a spune că unghiul este adimensional (tot un număr). Analiza procesuală a celor două obiecte abstracte implicate - arcul de cerc şi raza cercului respectiv - ne spune însă altceva. Raza cercului este un segment de dreaptă, deci un proces P₁ aşa cum am văzut până aici, dar arcul de cerc este un proces P₂. Cititorul este invitat să decidă singur dacă raportul a două procese de ordine diferite este adimensional.

 

Folosind noţiunile deja introduse în capitolul anterior de componente comune şi specifice (diferenţiale) ale unui obiect compus, vedem că variaţia r_X este componenta comună dintre variaţia r şi axa de referinţă X (axa faţă de care se evaluează direcţia unghiulară). Această componentă comună a două PES concurente (care au aceeaşi stare iniţială) dintre care unul este considerat ca referinţă, este proiecţia PES curent pe direcţia de referinţă.

 

 

în relaţia 4.4.5 funcţia simbolică C() este cea descrisă în par. 3.4 şi care reprezintă în cazul general funcţia de extragere a componentei comune dintr-o mulţime de obiecte abstracte, obiecte ce constituie argumentele funcţiei. în cazul obiectului compus r, componenta comună dintre vectorul r şi axa cu direcţia de referinţă X este:

r_X = r cosX                                            (4.4.6)

adică proiecţia vectorului r pe această axă[2].

PES r mai are o componentă r_Y pe direcţia axei independente Y, tot un PES dar care nu mai are comun cu axa de referinţă decât punctul de intersecţie, originea O, aşadar este o componentă disjunctă (specifică) a vectorului r faţă de axa de referinţă X.

 

 

Funcţia D() din relaţia 4.4.7 este funcţia de extragere a componentelor specifice ale unui obiect abstract faţă de componenta comună a unei mulţimi din care face parte obiectul respectiv (funcţie menţionată de asemenea în par. 3.4). Sensul pozitiv al variaţiei de direcţie este sensul pozitiv trigonometric, tot faţă de direcţia de referinţă a axei X din fig. 4.4.2.

 

Comentariul 4.4.2: Relaţia 4.4.7 este o consecinţă a unei legi pe care o vom discuta în cap. 9, dar am discutat-o pe scurt şi în capitolul anterior, conform căreia proprietăţile unui obiect ce aparţine unei mulţimi de obiecte sunt formate din două clase reunite de proprietăţi: proprietăţi comune tuturor obiectelor mulţimii şi proprietăţi specifice fiecărui obiect. Cu alte cuvinte, în cazul unui vector, faţă de o referinţă de direcţie V_R putem spune că obiectul vector este reuniunea (suma) celor două tipuri de componente:

 V = V_C + V_D                                                             (4.4.8)

Dar noi ştim că cele două componente ale unui vector ce satisfac relaţia 4.4.8 trebuie să fie reciproc perpendiculare (adică independente). Acesta este motivul pentru care componenta comună a unei mulţimi de vectori concurenţi este normală pe un plan ce include componentele lor specifice (faţă de componenta comună). O discuţie mai detaliată pe această temă în anexa X.15 şi X.17.

 

Componenta disjunctă a unui vector faţă de aceeaşi direcţie de referinţă va avea (în cazul unui spaţiu 3D) direcţia inclusă într-un plan normal pe referinţă (este tot o proiecţie a vectorului dar pe un plan normal pe direcţia de referinţă). O proprietate importantă a componentelor comună şi specifică a unui vector faţă de vectorul referinţă concurent este că toţi aceşti vectori sunt coplanari. Discuţia purtată pe seama unui PES bidimensional se poate extinde în acelaşi mod şi la vectorii tridimensionali, adăugându-se evident componenta după axa Z, dar problema este mai complicată şi nu o tratăm în acest paragraf deoarece scopul acestuia este doar de a lămuri cititorul asupra corespondenţei dintre un vector şi un PES.

Nu putem încheia această scurtă prezentare a reprezentărilor vectoriale pentru PES fără a face o precizare. Toate PES sunt reprezentabile prin vectori, dar nu toţi vectorii reprezintă PES, mai exact spus, există vectori care reprezintă doar direcţii de referinţă, fără a reprezenta şi variaţii de stare. O asemenea categorie de vectori sunt versorii axelor despre care am discutat pe scurt mai înainte, dar şi cei ce formează referinţele R locale ale unei curbe sau suprafeţe în spaţiu, tangenta, normala şi binormala. Aceşti vectori nu reprezintă PES ci numai direcţii de referinţă valabile în punctul lor de aplicare.