7.2.2 Modelul triadei de fluxuri

Fie un volum V mărginit de o suprafaţă reală de separaţie închisă , convexă şi fără găuri topologice, cu astfel de dimensiuni încât în acest volum să fie cuprinse toate elementele sistemului şi numai ele (fără elemente străine). Suprafaţa  va fi frontiera dintre două spaţii complementare[1] - cel interior cu volumul V şi cel exterior. Cu ajutorul acestei suprafeţe  putem defini trei clase de fluxuri:

1)   Fluxurile_, fluxuri deschise de intrare (imergente în V sau aferente lui V), ce traversează suprafaţa  de la exterior spre interior (fluxuri convergente sau fluxuri import);

2)   Fluxurile, fluxuri stocate (închise) în volumul interior V al sistemului;

3)   Fluxurile, fluxuri deschise de ieşire (emergente din V sau eferente lui V), ce traversează suprafaţa  de la interior spre exterior (fluxuri divergente sau fluxuri export).

Comentariul 7.2.2.1: Cu toate că este destul de neplăcut şi plicticos, menţionarea tuturor denumirilor fluxurilor implicate în transferul printr-o SRS este importantă pentru început deoarece în anumite lucrări sunt folosite numai unele din denumiri, dar fiind vorba de un model general, aceste denumiri specifice unui anumit domeniu profesional se dovedesc similare cu altele din alte domenii. Până la "standardizarea" unei singure denumiri pentru fiecare tip de flux va trebui să le menţionăm pe toate. De asemenea, în categoria fluxurilor eferente vor intra aşa cum vom vedea mai încolo şi fluxurile ce nu provin din interiorul volumului V ci de la suprafaţa acestuia (fluxurile reflectate); important este că şi aceste fluxuri reflectate sunt deschise şi au sensul spre exteriorul volumului V la fel ca şi fluxurile emergente, fiind tot fluxuri de ieşire (divergente). Dacă cititorul are cunoştinţe de teoria câmpurilor vectoriale, atunci poate observa imediat că cele două clase de fluxuri de intrare şi ieşire (mai exact componentele lor normale pe SRS) vor avea divergenţa diferită de zero (pozitivă sau negativă) şi rotor nul, în timp ce componentele coerente ale fluxurilor stocate care au o circulaţie nenulă vor avea divergenţă nulă (prin ) şi rotor nenul. în acest mod, modelul triadei de fluxuri "conectează" între ele cele două clase fundamentale de fluxuri (cele cu divergenţă nenulă şi cele cu rotor nenul) care până acum păreau să nu aibă nicio legătură.

Stocul de atribut de tip k existent la un moment t şi care este conţinut într-un flux stocat în interiorul unui SM este dat de relaţia:

                                                                 (7.2.2.1)

unde  este VDF al fluxului de intrare de tip k, iar  cel al fluxului de ieşire, adică stocul intern al unui anumit atribut este diferenţa dintre "istoria" afluxurilor şi a celei a efluxurilor din sistem, istorie ce începe de la momentul t₀, momentul formării sistemului material, moment ce coincide cu apariţia (noi spunem generarea) fluxurilor stocate .

Există pentru un anumit tip de SM un flux stocat  ce conţine un stoc numit stoc de model Q_kr, stoc de referinţă al atributului (mărimii) de tip k, faţă de care fluxul real stocat la un anumit moment poate fi mai mare sau mai mic. Diferenţa:

                                                                                                   (7.2.2.2)

reprezintă cererea (necesarul) de flux de tip k dacă semnul diferenţei este negativ (fluxul stocat este mai mic decât stocul de model), şi excesul (surplusul) de flux de tip k dacă semnul este pozitiv.

Comentariul 7.2.2.2: De exemplu la om, cererea de flux de apă se manifestă prin semnalul dat de SPI intern, senzaţia de sete, cu intensitate proporţională cu necesarul (cererea) de flux ; la completarea acestui necesar, excesul de flux este semnalat prin senzaţia de saţietate. Aceeaşi situaţie se manifestă în cazul cererilor de flux de oxigen, de hrană etc. diferind doar semnalul dat de SPI.

Din p.d.v. cauzal, fluxul stocat [2] (al cărui VDF îl notăm cu ) este efectul acumulării fluxului de intrare  şi sursa (cauza) fluxului de ieşire . între fluxurile ce formează o triadă există (în situaţia de echilibru, adică de menţinere a stocului unui atribut intern k egal cu stocul său de model), relaţia fundamentală de conservare:

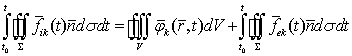                                           (7.2.2.3)

unde t₀ este cum spuneam mai sus, momentul apariţiei (formării) SM şi t este momentul curent (prezent). Relaţia 7.2.2.3 ne spune că stocul de atribut k ce este conţinut în fluxul intern (tot de tip k) al SM la momentul prezent t, este dat de integrala temporală a intensităţii afluxurilor, minus integrala temporală a intensităţii efluxurilor, pe intervalul temporal de existenţă a SM. în condiţii de echilibru permanent a triadei fluxurilor (adică menţinerea invariantă a stocurilor interne egale cu cele de model), relaţia 7.2.2.3 poate fi scrisă simplificat:

                                                                                              7.2.2.4)

unde ,  şi  sunt distribuţiile Euler ale fluxurilor de tip k de intrare, interne şi de ieşire la un anumit moment t, distribuţii pe suprafaţa  pentru fluxurile de intrare/ieşire şi pe volumul V pentru fluxurile stocate.

Fluxurile interne stocate în interiorul sistemului sunt fluxurile vitale (funcţionale) ale SM, prin care noul SM format se deosebeşte de mediul de referinţă din care a luat naştere (mediul ce conţine mulţimea generatoare a elementelor structurale ale SM). în momentul dispariţiei acestor fluxuri, dispare (moare) şi sistemul.

Proprietăţile comune ale tuturor SM sunt cele rezultate din modelul general de SM - modelul triadei de fluxuri (modelul 3F). Acest model stabileşte că orice SM are un volum interior finit, separat de exteriorul său de o suprafaţă reală de separaţie (SRS), ce conţine fluxurile închise ale SM. SRS este traversată în ambele sensuri de celelalte două categorii de fluxuri ale modelului - fluxurile de intrare şi cele de ieşire. Existenţa fluxurilor ca procese distribuite de mişcare determină existenţa inseparabilă a unei proprietăţi fundamentale a SM, ce reprezintă mişcarea - energia - iar existenţa fluxurilor stocate (mai exact spus a stocurilor pe care acestea le conţin) este un factor determinant pentru alte două proprietăţi fundamentale ale SM - structura spaţială şi inerţia. Aceste proprietăţi fundamentale vor fi analizate mai încolo, deocamdată ne vom ocupa de SRS deoarece înţelegerea acestui concept este foarte importantă.